[확률및통계] 조건부확률과 Bayes 정리

본 게시물의 내용은 '확률 및 통계(이상화 교수님)' 강의를 듣고 작성하였다.

 

1) Sample Space → S(set)

: output이 랜덤하게 나올때, 가능한 모든 전체 집합.

2) Event (A) → A⊂S

: P(A) = probability (outcome ∈ A) : A가 발생할 확률, 정확하게는 특정하게 outcome을 뽑았을때 이것이 A에 포함될 확률

 

3) Conditional Probability (조건부확률)

: P(B|A) : A라는 조건이 발생했을 때, B라는 Event가 발생했을 때의 확률

4) Total probability

: \(P(A) = P(A_1) + P(A_2) + ... + P(A_n)\)
A라는 사건이 발생할 확률을 구하는데, A라는 사건을 서로간에 중복이 되지 않는 배반사건으로 나눠서 각각의 확률의 합으로 구한다.
배반사건을 구할 때는 \({A_1, A_2, ... , A_n}\) : partition of S 이다.
=> \(P(A_1) = P(A_1 \cap A) = P(A|A_1)P(A_1)\) 이므로 \(P(A) = \sum_{i=1}^nP(A|A_i)P(A_i)\)

 

5) Bayesian Theorem

: 조건의 서로 위치를 바꿔가면서 문제를 푸는 기본적인 수학적 방법

A,B 순서를 바꾸면 이와 같다.

A : observation data(이미 관측한 데이터), \(A_i\) : (unknown) original input

 

 

6) Independent Events

if A and B are (mutually) independant, \(P(A \cap B) = P(A)P(B)\)
서로 간에 영향을 주지 않는 관계, 이 경우는 repeated (restored) trials(반복적인 복원 실험)에서 사용한다.
ex) 빨간색 공 4개, 흰색공이 3개가 들어있는 주머니가 있다. 이때, 1개를 꺼냈을 때 흰공이 나올지, 빨간공이 나올지 확률을 구한다. 이때, 꺼낸 공을 다시 넣으면 restored (복원), 다시 넣지 않고 확률을 구하는 경우도 있음.

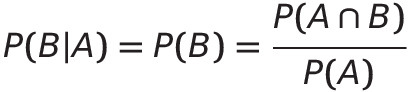
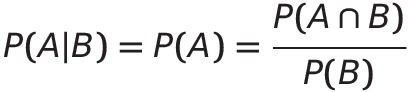
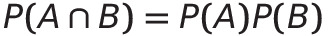
ex) 오늘의 날씨를 예측하는 확률값을 구할 때, 어제의 날씨, 그저께의 날씨로 오늘의 날씨를 계산될 수 있다. 한 30일 전의 날씨는 오늘의 날씨를 예측하는데 영향을 끼치지 않는다. 이는 independant 하다고 본다.

\(P(W_t)\) : today의 날씨(weather), t-1 : 어제, t-2 : 그저께

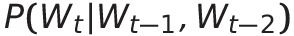
* Independent ≠ exclusive
두 개의 Event가 서로 독립인 것과, 공통된 요소가 없다는 것(교집합X)은 아예 다른 의미이다.

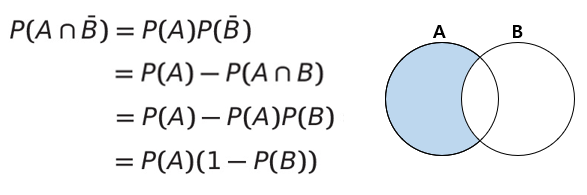
* If A and B are independent,
\(A\), \(\bar{B}\) 는 independent
\(\bar{A}\), \(B\) 는 independent
\(\bar{A}\),  \(\bar{A}\) 는 independent
(\(\bar{A}\) : A의 여집합(complement))

\(A\), \(\bar{B}\) 는 independent하다는 증명

 

7) Combined Experiments

: 독립적인 2가지 사건의 Sample Space S1, S2가 있을 때, 이 둘을 합쳐서 요소들을 묶어 원소쌍으로 만든다.
for two experiments with \(S_1\), \(S_2\)
S = \(S_1\ × S_2\) (× : Cartesian product )
= {\((x_i, y_j) | x_i ∈ S_1, y_j ∈ S_2 \)}