[선형대수학] 인공지능을 위한 선형대수 (10) - 끝

본 게시물의 내용은 '인공지능을 위한 선형대수(주재걸 교수님)' 강의를 듣고 작성하였다.

해당 글은 아래의 8가지를 다룬다.
1. 특이값 분해(Singular Value Decomposition)
2. 스펙트럴 정리(Spectral Theorem)
3. 대칭행렬(Symmetric Matrix)
4. Positive Definite Matrix
5. 주성분분석(Principal Component Analysis)
6. 그람행렬(Gram Matrix)
7. Low-Rank Approximation
8. Dimension-Reducing Transformation

 

- 특이값 분해 Ⅰ

- 특이값 분해(Singular Value Decomposition, SVD)
: 직사각행렬 A를 대상으로 $A=U\Sigma V^T$로 분해하는 것을 의미한다. 여기서 U, V 행렬은 정사각행렬로 orthonormal column들을 갖고 있고, Σ는 직사각행렬로 diagonal 행렬이다(정확하게는 정사각행렬이 아니므로 대각행렬은 아니다, 대각성분이 존재하고 나머지 값은 0인 행렬이다)

 

$A=U\Sigma V^T$의 식을 Sum of Outer Product를 사용해서 변형해보면, 상수값 σ는 순서가 상관없으므로 u, σ, $v^T$의 곱의 합들으로 나열되어 표현된다.

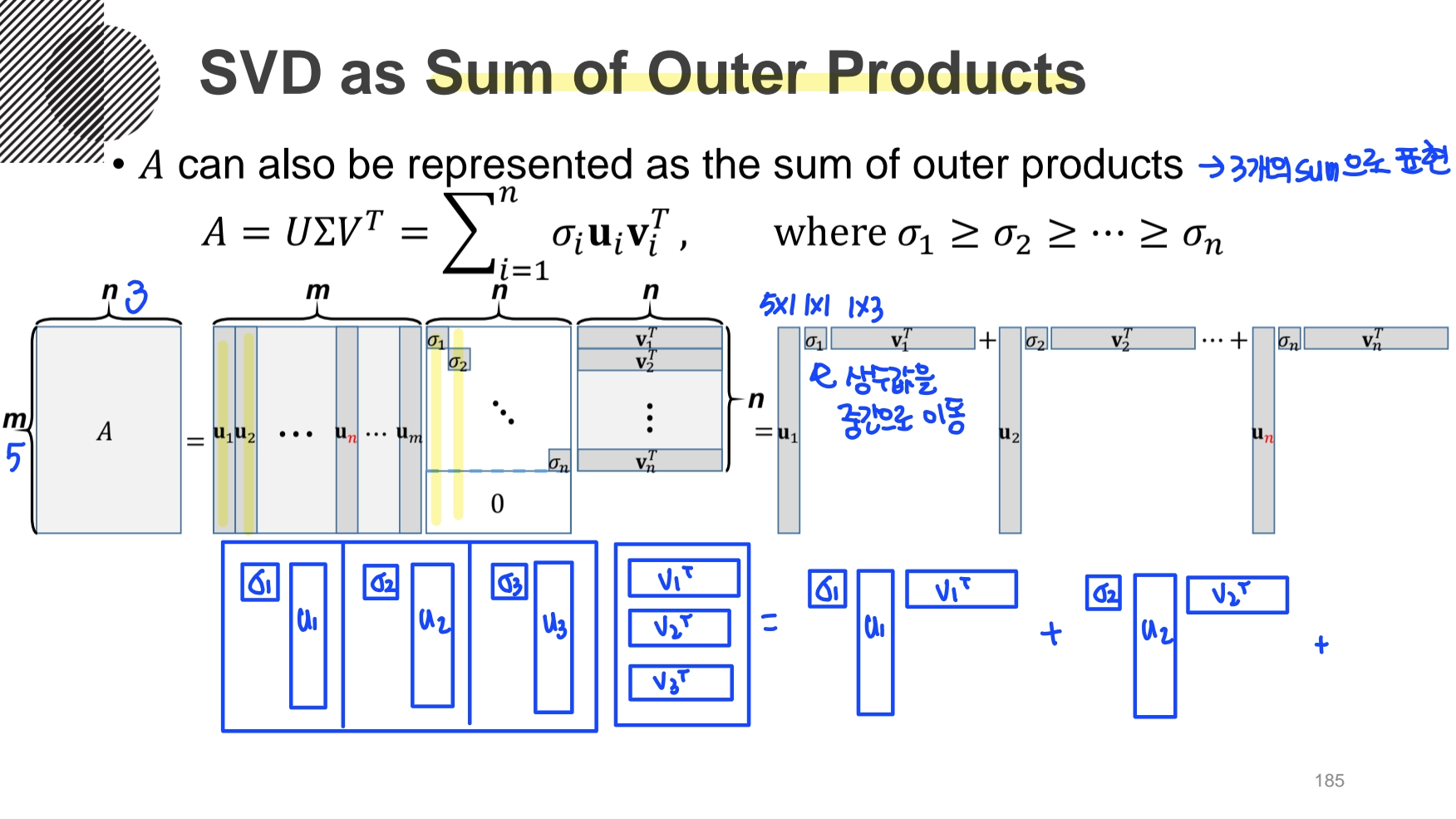
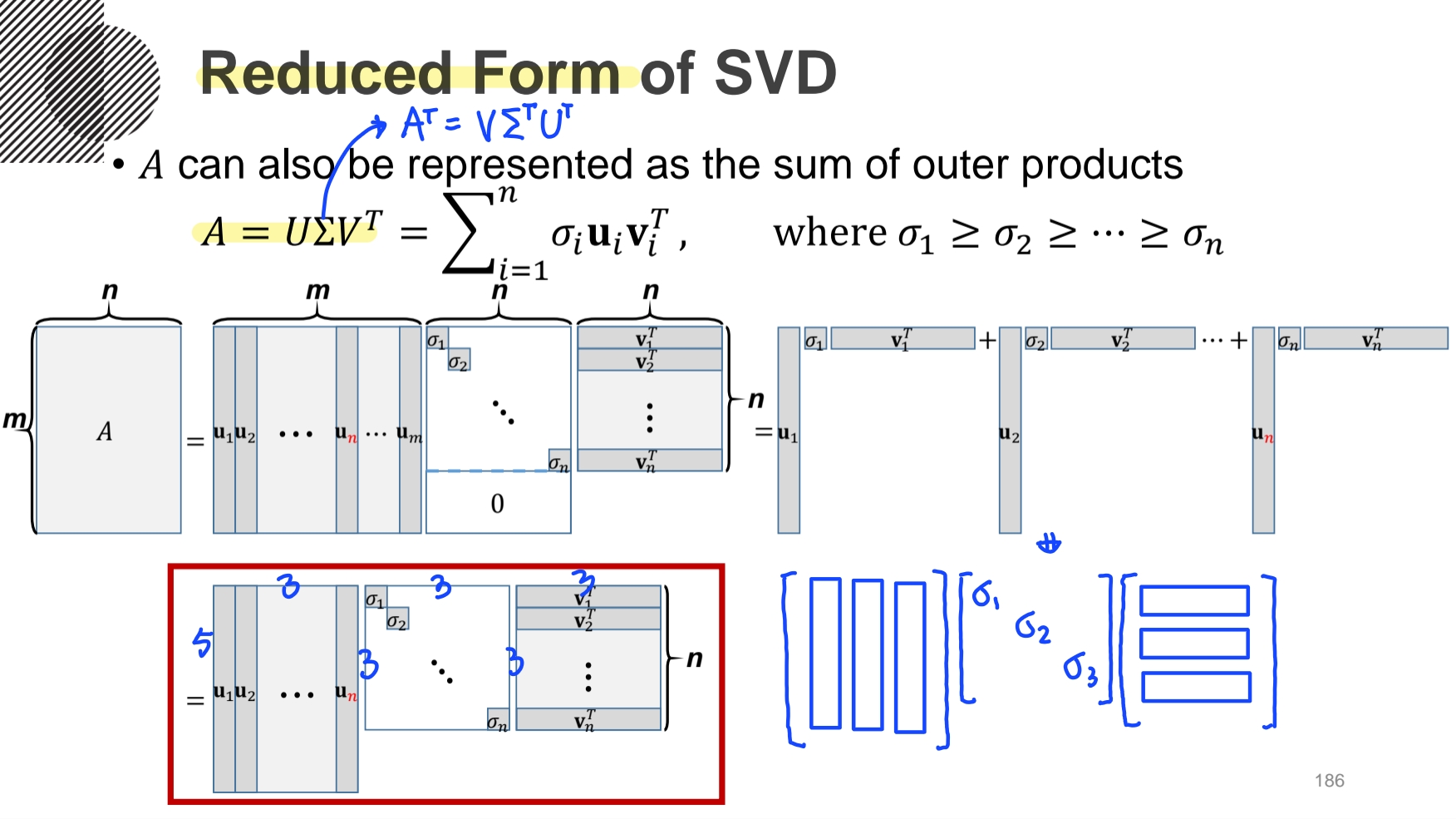
그리고, 이것을 선형결합으로 다시 표현해보면, Reduced Form 하게 표현된 걸 볼 수 있다.

Gram-Schmidt orthogonalization을 사용해서 A, $A^T$의 orthonormal basis를 2개 찾을 수 있다.
그런데, orthonormal basis가 유일하지 않다. 왜냐하면, Gram-Schmidt orthogonalization 방법은 순서에 맞게끔 진행이 되는데, 순서가 변동되면 결과값도 달라지기 때문이다.
그래서, AV = ΣU = UΣ (Σ행렬의 상수값 σ는 순서 상관없음) 의 특정한 조건을 만족시키는 orthogonal basis를 찾는 방법을 사용한다.

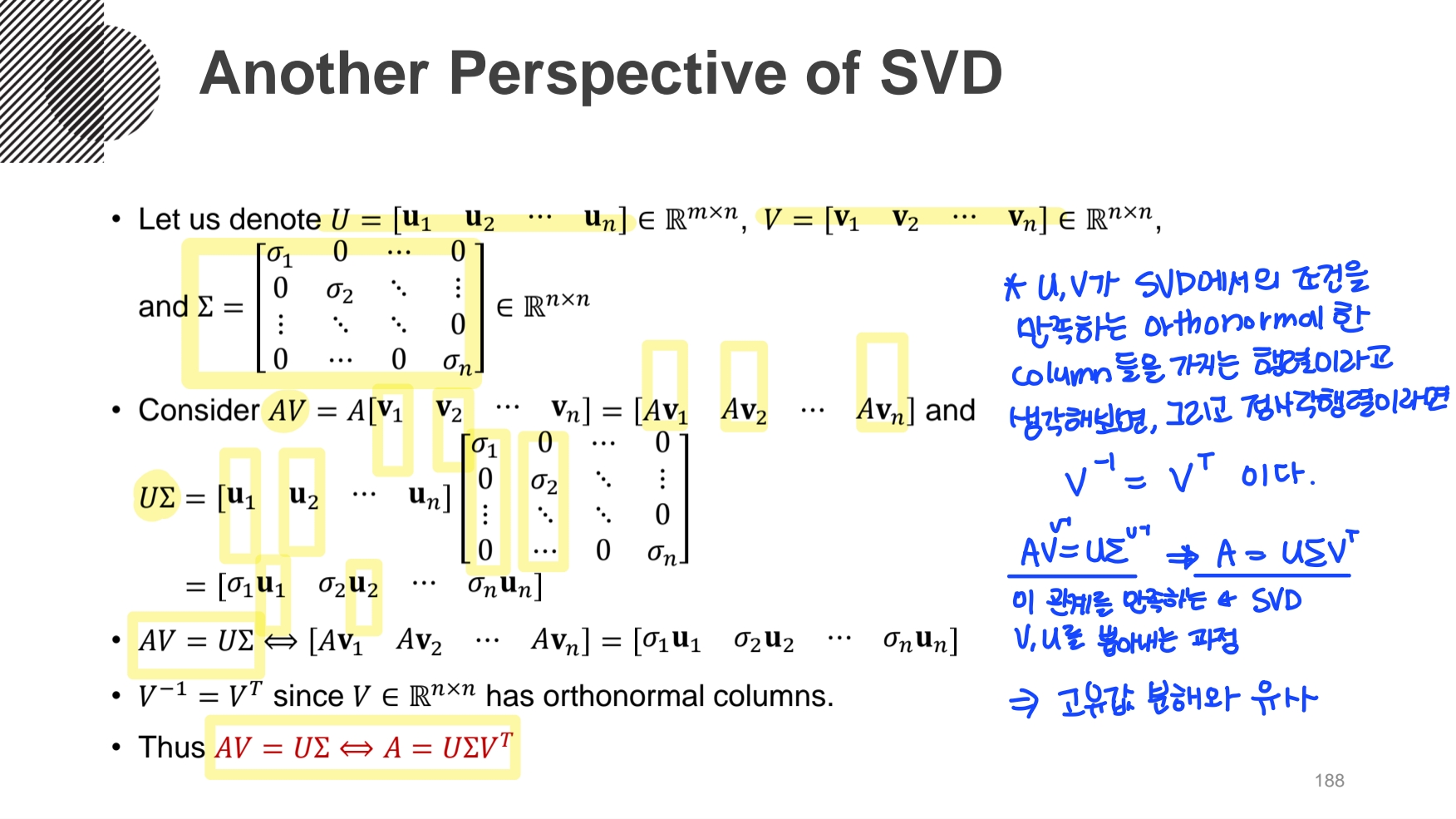
\(AV=UΣ\)의 식 양변에 $V^{-1}$을 곱하면 $A=U\Sigma V^T$가 나온다.($V^{-1}=V^T$이므로) 이런 연산은 고유값 분해와 유사하다.

- 특이값 분해 Ⅱ

SVD를 계산하기 위한 알고리즘이 따로 있는 것이 아니라, 안을 들여다보면 eigendecomposition(고유값분해)으로 푸는 것이다. $A{A}^T$와 $A^{T}A$를 계산해보면 고유값분해 형태($A=VD{V}^{-1}$)와 굉장히 유사하다.
다만, 여기서 아래의 3가지 조건을 만족하는 U, V, Σ를 찾을 수 있어야 한다.
1) Spectral theorem : $A{A}^T$와 $A^{T}A$에서 각각 n개의 orthonormal한 고유벡터를 찾을 수 있어야 한다.
2) Positive definite : $A{A}^T$와 $A^{T}A$에서 찾은 고유벡터는 모두 0보다 커야한다. (양수)
3) $A{A}^T$와 $A^{T}A$의 고유벡터들은 같아야 한다.

- Symmetric
: 행렬의 대각선을 기준으로 데칼코마니인 것을 의미한다.
Symmetric은 행렬 A를 전치해도 똑같은 $A=A^T$ 이므로
$A{A}^T$와 $A^{T}A$는 $(A{A}^T{)}^T=A{A}^T$ 이고, 반대로도 똑같으므로 둘은 Symmetric하다.

Symmetric 행렬 S는 항상 diagonalizable 가능하다. 즉, eigencomposition이 무조건 존재한다.
그리고 고유벡터들은 선형독립이고, orthogonal 하다.

- Spectral Theorem
: Symmetric 행렬 S를 $S=UD{U}^{-1}$로 대각화 과정을 통해 분해할 수 있다.
Symmetric 행렬 S는 n개의 실수로 이루어진 고유벡터를 가진다. (중근포함) 그리고 이는 orthogonally하게 diagonalizable 가능하다

- Positive Definite Matrice
: 정사각행렬 A가 있을 때, $x^{T}Ax$의 어떤 x를 넣어도 항상 양수값인 것을 의미한다.
- Positive semi-definite Matrice
: Positive Definite Matrice에서 0이 될 때도 포함되는 것을 의미한다.

행렬 S가 symmetric하고 positive-definite하다면, Spectral decomposition이 가능하다.
그리고 여기서 모든 고유값은 양수가 된다.

$A{A}^T$와 $A^{T}A$는 Symmetric positive-(semi-)definite 한가? 그렇다.
$(A{A}^T{)}^T=A{A}^T$와 $(A^{T}A{)}^T=A^{T}A$을 통해 Symmetric을

$x^{T}A{A}^{T}x=||A^{T}x|{|}^2>=0$으로 Positive-(semi-)definite 임을 알 수 있다.

따라서, orthogonal eigenvector로 구성된 U, V 행렬을 구성할 수 있고, S의 Eigenvalue들이 모두 양수로 구성되어 있음을 알 수 있다.

- 어떤 직사각행렬이든 SVD는 항상 존재한다.

- 어떤 정사각행렬은 Eigendecomposition이 없을 때도 있지만, SVD는 항상 존재한다.

cf) Eigendecomposition은 정사각행렬에서만 정의 가능 했음.

 

결론 : 주어진 행렬이 Square, Symmetric, Positive-(semi-)definite 조건을 만족한다면, Eigendecomposition이 항상 존재하고, Eigendecomposition와 Singular Value Decomposition은 사실상 같은 역할을 한다.

 

 

 

- 고유값 분해와 특이값 분해의 응용

머신러닝에서 우리가 다루는 데이터는 Symmetric positive-(semi-)definete matrix인 경우가 대부분이다.

feature(키, 혈액형, 몸무게)-by-data item(사람)인 행렬 A를 생각해보면

$A^{T}A$는 data item-by-data item matric로 두 사람간의 유사도(similarity)를 계산하는 것,

$A{A}^T$는 feature-by-feature로 두 feature간의 유사도(similarity)이므로 즉, 상관관계를 나타내는 것이다.

 

이러한 유사도와 상관계수를 통해 PCA(pricipal component analysis)를 진행할 수 있고,

style transfer을 해결할 때 Gram matrix을 사용하는데, 이게 $A{A}^T$의 역할과 같다.

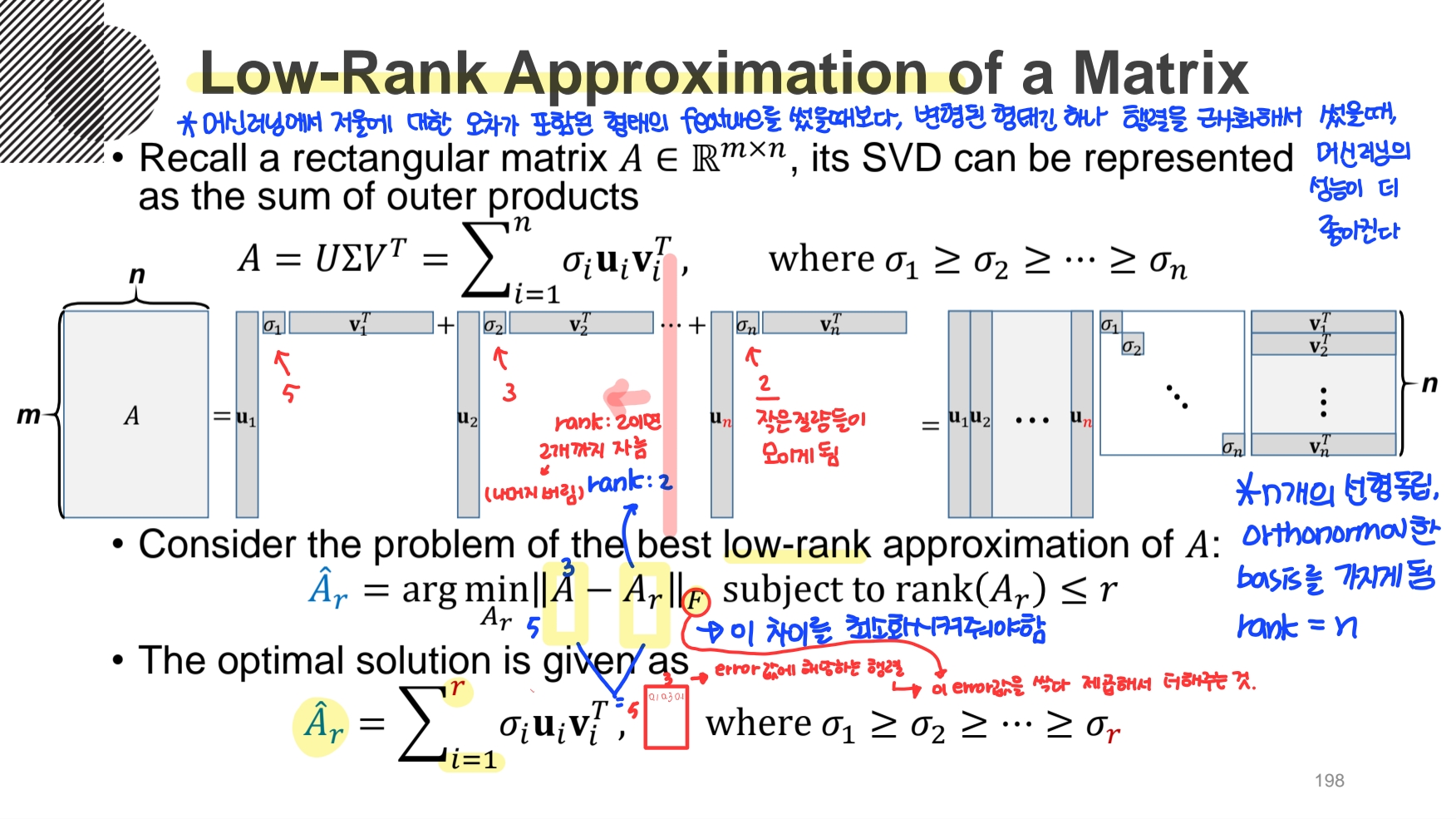
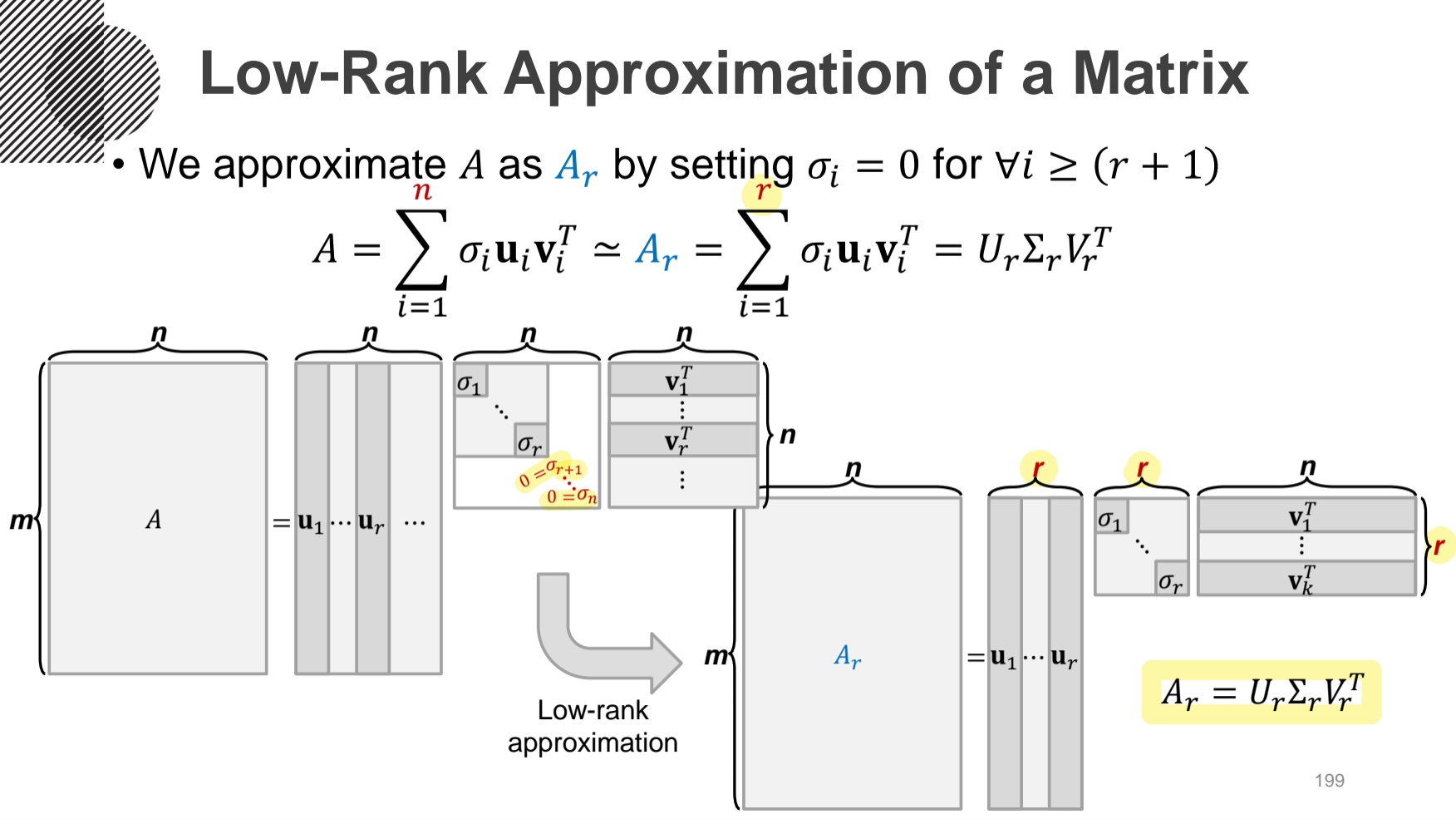
앞에서 SVD를 Sum of Outer Product로 Reduced Form 하게 표현될 수 있었다. 이때 발생하는 문제는 Low-Rank Approximation 이다. 이는 행렬의 Rank에 제약을 두면서 원래의 행렬과 가장 비슷한 행렬을 찾는 문제이다. 근사한 행렬이 원래의 행렬과 얼마나 비슷한지는 Norm을 사용해서 구하며, 이 차이를 최소화해주어야 한다. 식은 위와 같다.

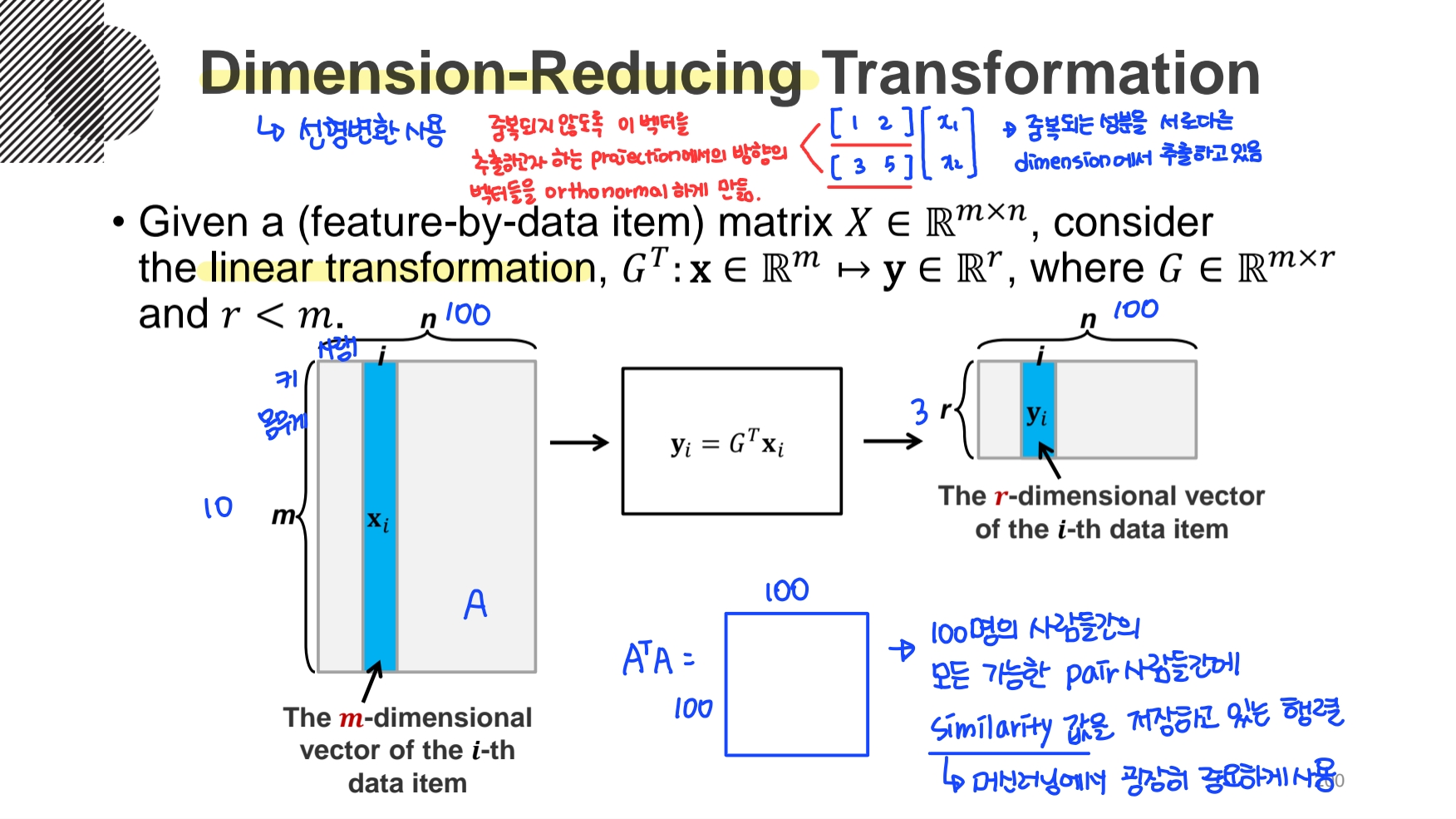
feature-by-data item 행렬 X(mxn)를 m개의 feature에서 r개의 feature만 사용하도록 줄이는 것을 Dimension-Reducing Transformation 이라 한다. 이때 변환은 선형변환을 사용한다.

보통 어떤 Feature의 두 열의 정보가 대게 중복되어 있으므로, 이러한 중복된 정보를 제거하기 위해서는 orthonormal하게 만들어서 pairwise similarity를 가장 잘 보존하도록하는 차원축소된 버전의 표현형을 얻으면 된다. 식은 와 같다.

SVD는 PCA, Topic modeling, word2vec, gram matrix 등 많은 분야에서 사용되고 있다.