코딩하는 해맑은 거북이
[선형대수학] 인공지능을 위한 선형대수 (7) 본문
본 게시물의 내용은 '인공지능을 위한 선형대수(주재걸 교수님)' 강의를 듣고 작성하였다.
해당 글은 아래의 2가지를 다룬다.
1. 그람-슈미트 직교화(Gram-Schmidt Orthogonalization)
2. QR분해(QR Factorization)
- 그람-슈미트 직교화

- 그람-슈미트 직교화(Gram-Schmidt Orthogonalization)
: 수직이 아닌 선형독립한 2개의 벡터를 orthogonal basis 벡터로 만드는 것.
(지난 게시글에서 언급한 정사영(Orthogonal Projection)을 통해 구한다.)

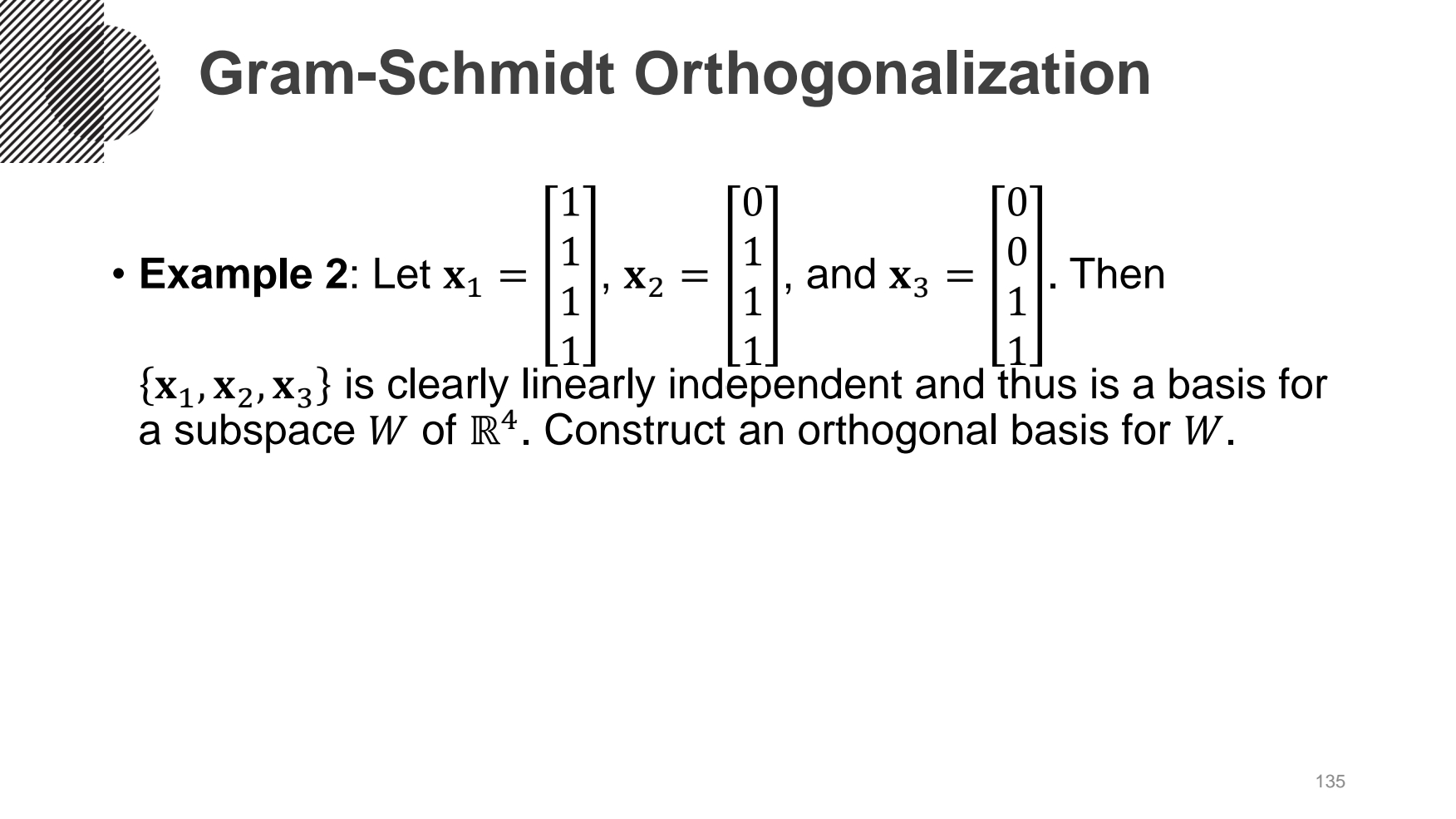
수직이 아닌 선형독립한 2개의 벡터(v1, v2)를 orthogonal basis 벡터(u1, u2)로 만드는 예시를 진행해보았다.
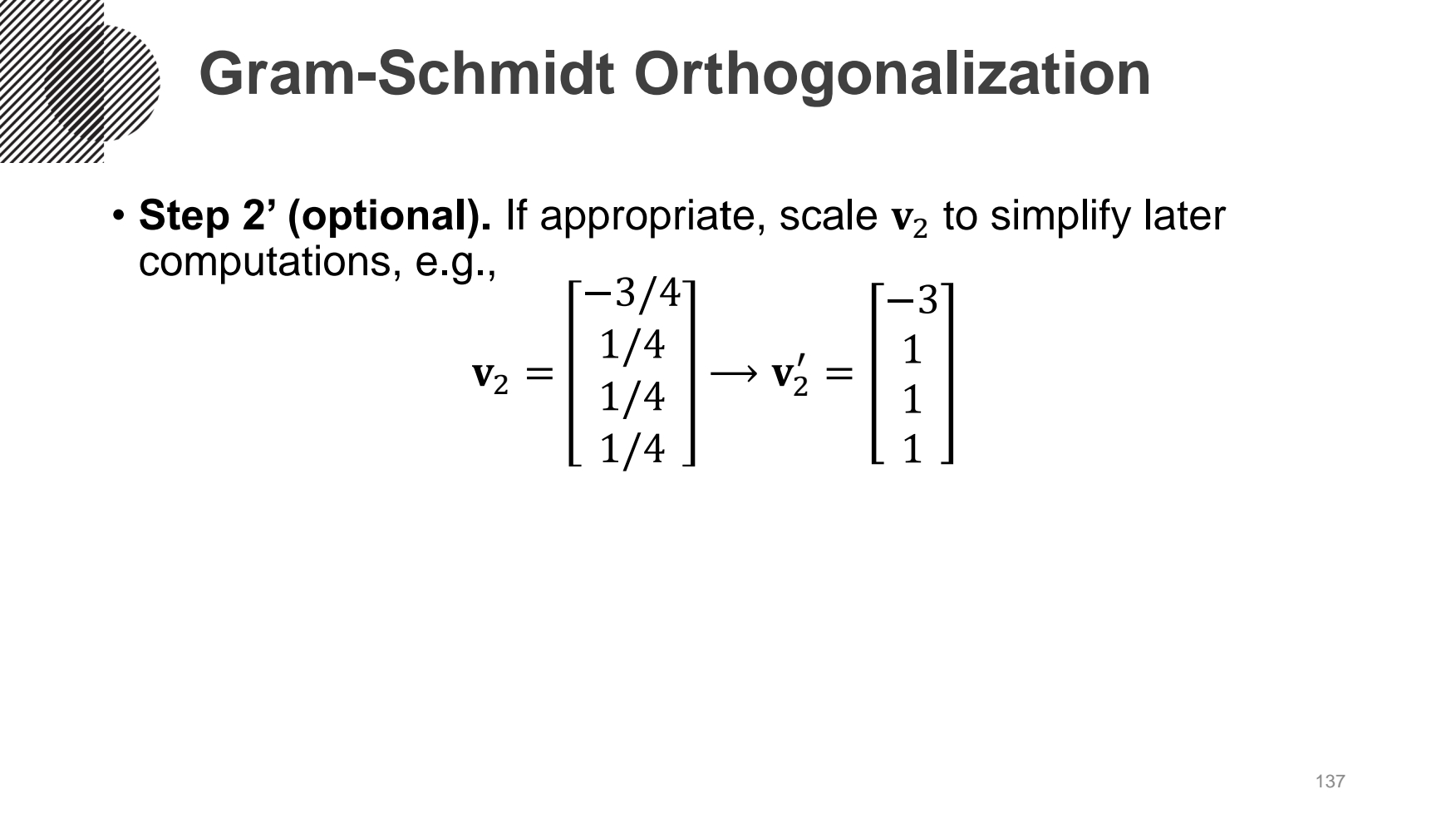
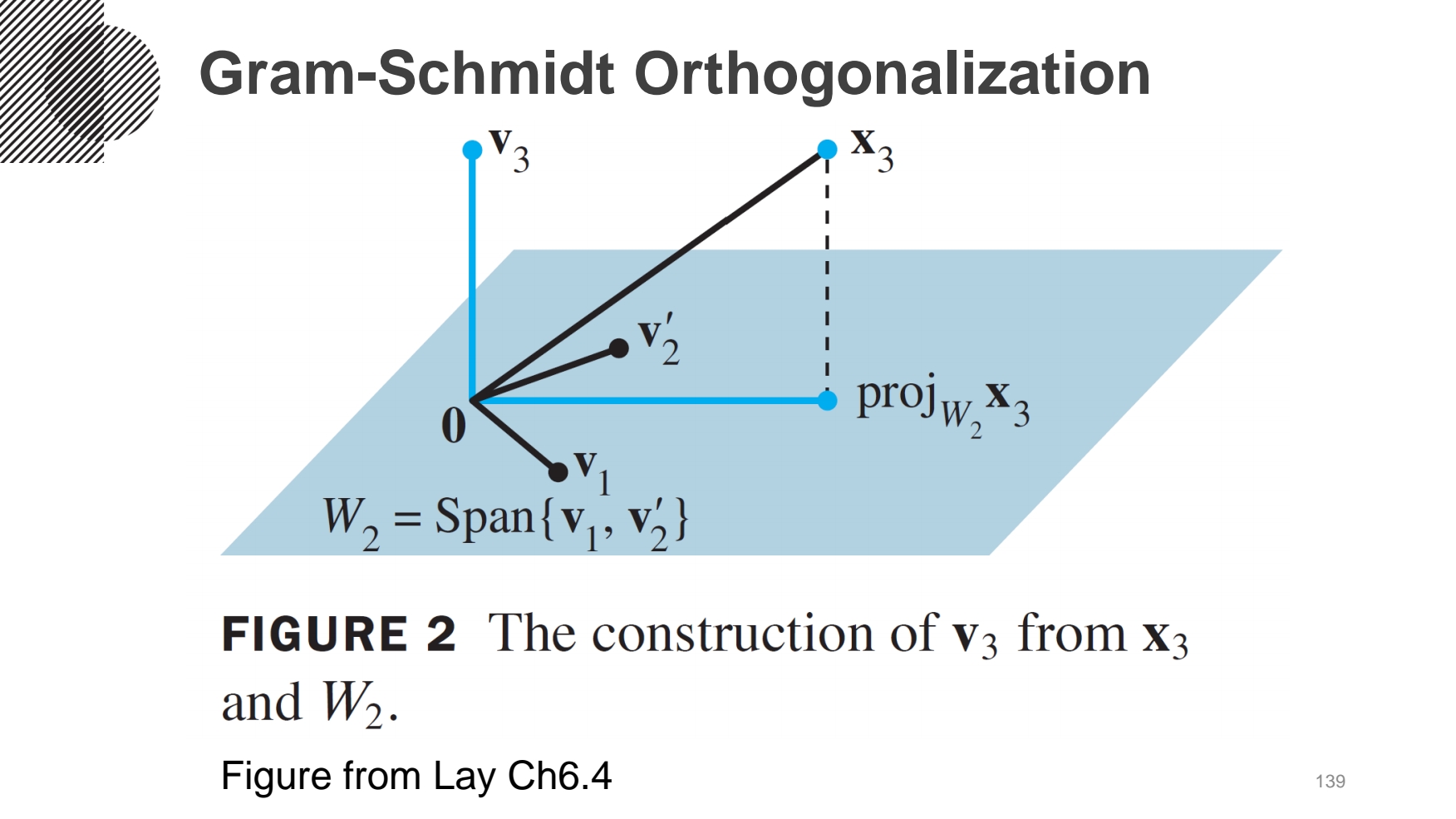
첫번째 column 벡터인 u1은 v1을 normailzation 한 값을 쓰고, 두번째 이상 column 벡터부터는 앞의 벡터들의 영향을 받으므로 각각의 벡터에 projection한 값을 빼서 구한다. 즉, u2 = v2-(v2·u1)xu1 으로 구한다. 이때 Span{v1, v2} = Span{u1, u2}이다.


- QR분해

- QR Factorization
앞서 언급한 그람-슈미트 직교화(Gram-Schmidt Orthogonalization)를 통해 orthogonal basis 행렬(Q)을 만들었다. 이 행렬과 원래의 input 행렬(A)을 통해 원래의 input 행렬로 복원하기 위한 선형결합의 계수들의 행렬(R)을 구하는 것이다.
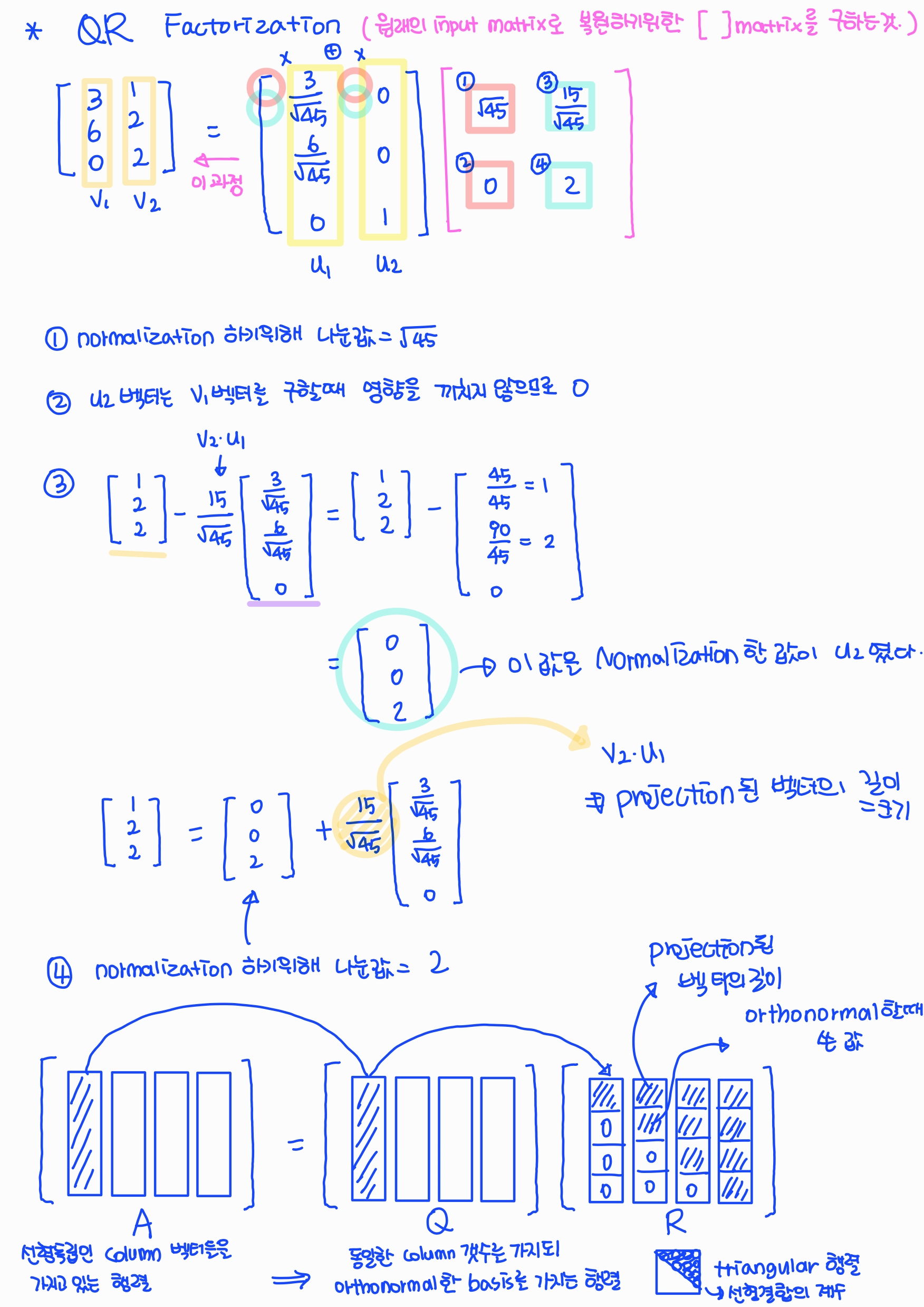
위의 예시에서 R 행렬을 번호 순서대로 구해보면,
1) v1을 normailzation 하기 위해서 나눴던 값이다.
2) u2 벡터를 구할 때, v1의 영향이 없었으므로 0이다.
3) 이전에 u2을 구하기 위해서 u2 = v2 - (v2·u1)xu1 을 진행하고 normalization을 했다.
그럼 원래의 값 v2로 돌아가기 위해 u2 + (v2·u1)xu1 을 진행하면 된다. 그리고 u1과 계수값으로 곱해지므로 (v2·u1)이다.
4) u2를 구할 때, 진행했던 normalization 하기 위해 나눴던 값이다.
A 행렬은 선형독립인 Column 벡터들을 가지고 있는 행렬이다.
Q 행렬은 A 행렬과 동일한 Column 갯수를 가지되 orthonormal basis를 가지는 행렬이다.
R 행렬은 선형결합의 계수들을 모은 triangular 행렬이다.






'Mathematics | Statistics' 카테고리의 다른 글
| [선형대수학] 인공지능을 위한 선형대수 (9) (0) | 2022.07.22 |
|---|---|
| [선형대수학] 인공지능을 위한 선형대수 (8) (0) | 2022.07.21 |
| [선형대수학] 인공지능을 위한 선형대수 (6) (0) | 2022.07.19 |
| [선형대수학] 인공지능을 위한 선형대수 (5) (0) | 2022.07.18 |
| [선형대수학] 인공지능을 위한 선형대수 (4) (0) | 2022.07.17 |




