코딩하는 해맑은 거북이
[선형대수학] 인공지능을 위한 선형대수 (6) 본문
본 게시물의 내용은 '인공지능을 위한 선형대수(주재걸 교수님)' 강의를 듣고 작성하였다.
해당 글은 아래의 3가지를 다룬다.
1. Orthogonality와 Orthonormality
2. 직교기저(Orthogonal Basis)와 정규직교기저(Orthonormal Basis)
3. 정사영(Orthogonal Projection)
- Orthogonal Projection Ⅰ

- Orthogonal Projection(정사영)
: '수직으로 투영된 그림자'를 말한다. 이때 내려진 수선의 발이 행렬과 주어진 입력벡터의 곱으로 나타남으로 선형변환이다.

- orthogonal set
: 집합 내의 모든 벡터들이 서로 수직인 벡터의 집합이다.
- orthonormal set
: orthogonal set에서 길이만 1로 바꾼 벡터의 집합이다.
* orthogonal set은 선형독립이다.

basis로 부터 orthogonal basis를 만들기 위해선 Gram-Schmidt process(Gram-Schmidt orthogonalizaiton) 방법을 사용한다. 이 방법을 통해 행렬로 분해할 수 있는데 그것을 QR factorization 이라 한다.
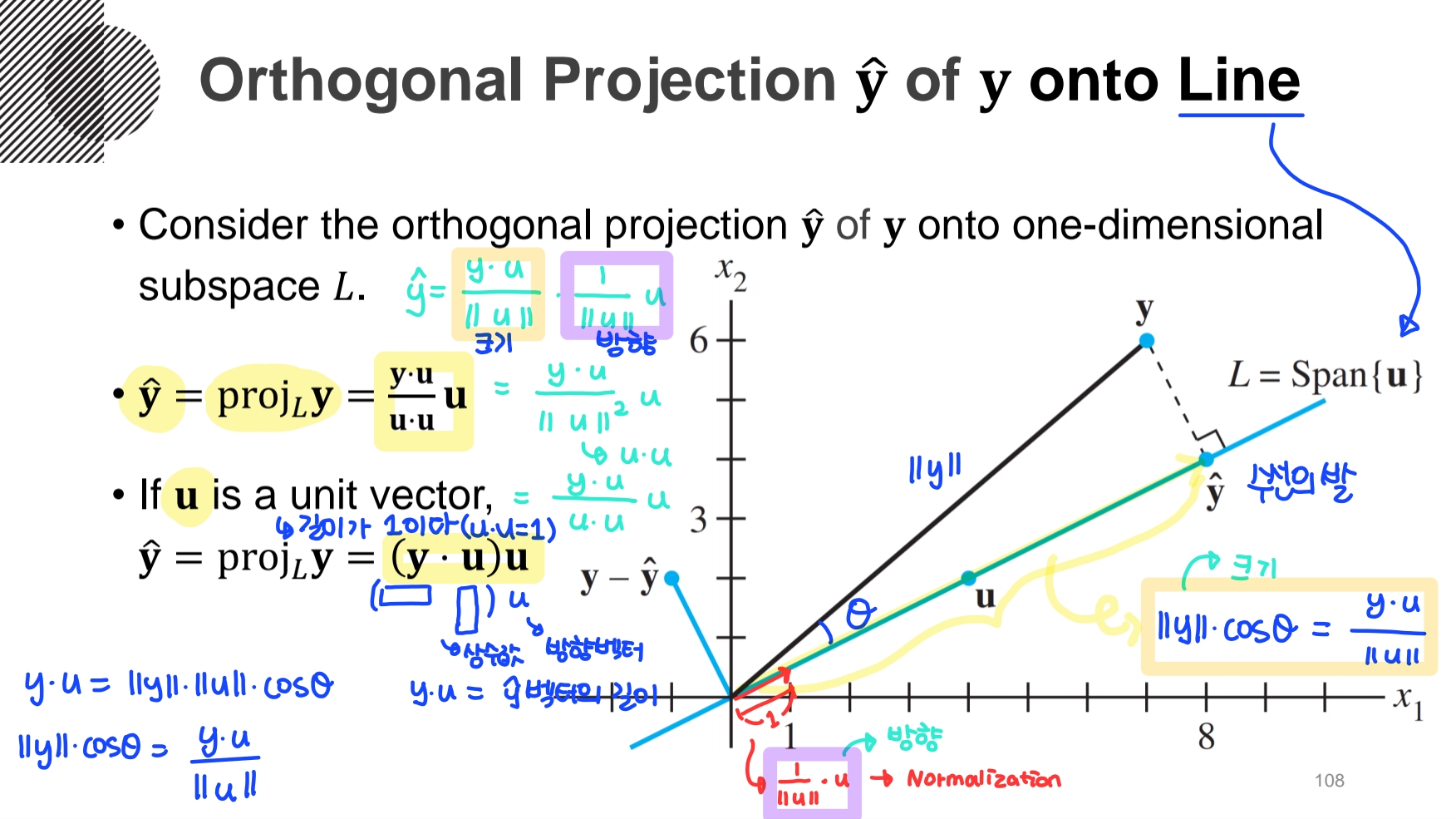
- 1차원 subspace L의 Span은 Line이다. Line으로의 orthogonal projection은 u벡터에 수선의 발을 내렸을 때의 크기와 방향을 곱해서 구한다.
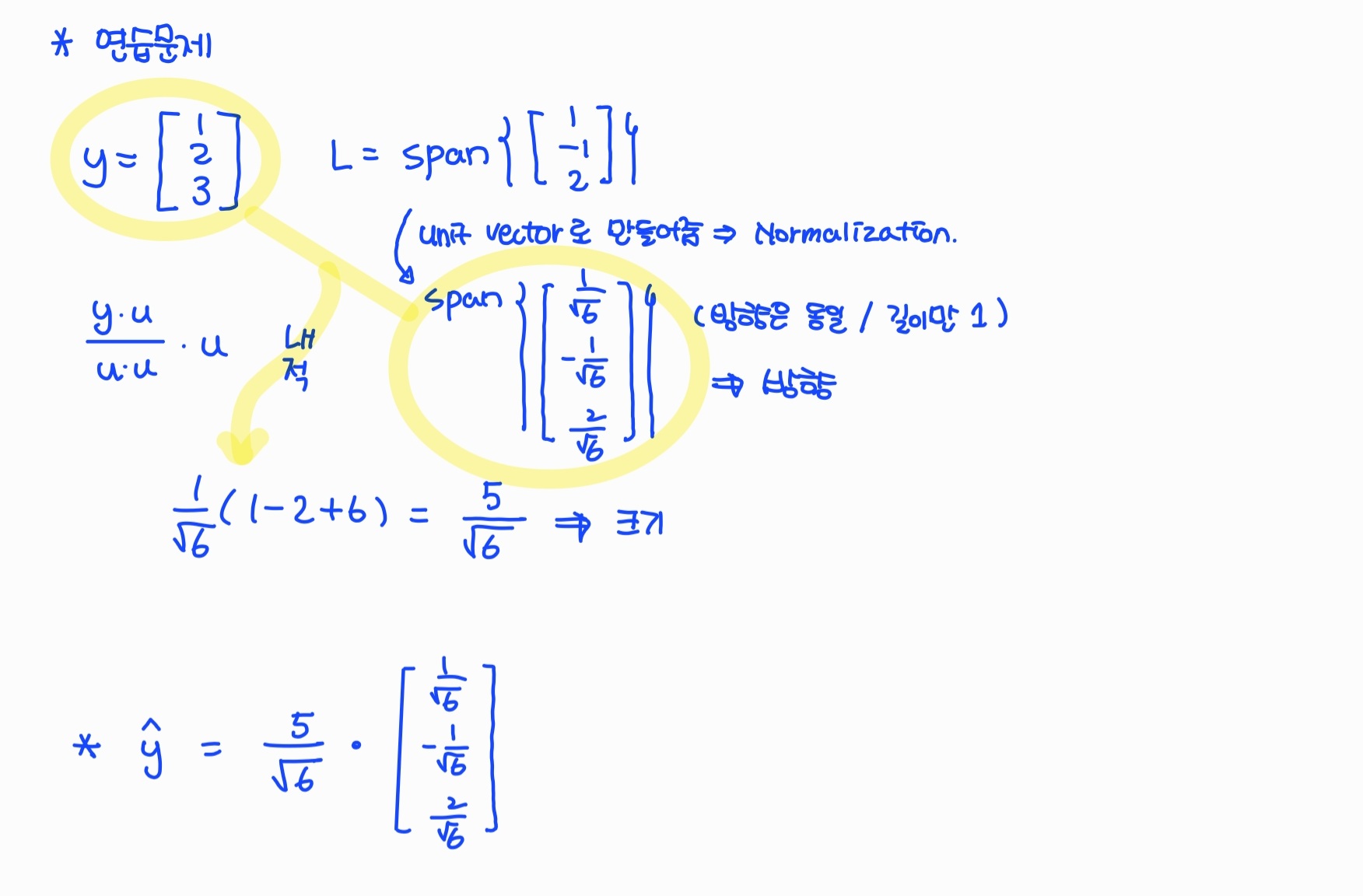
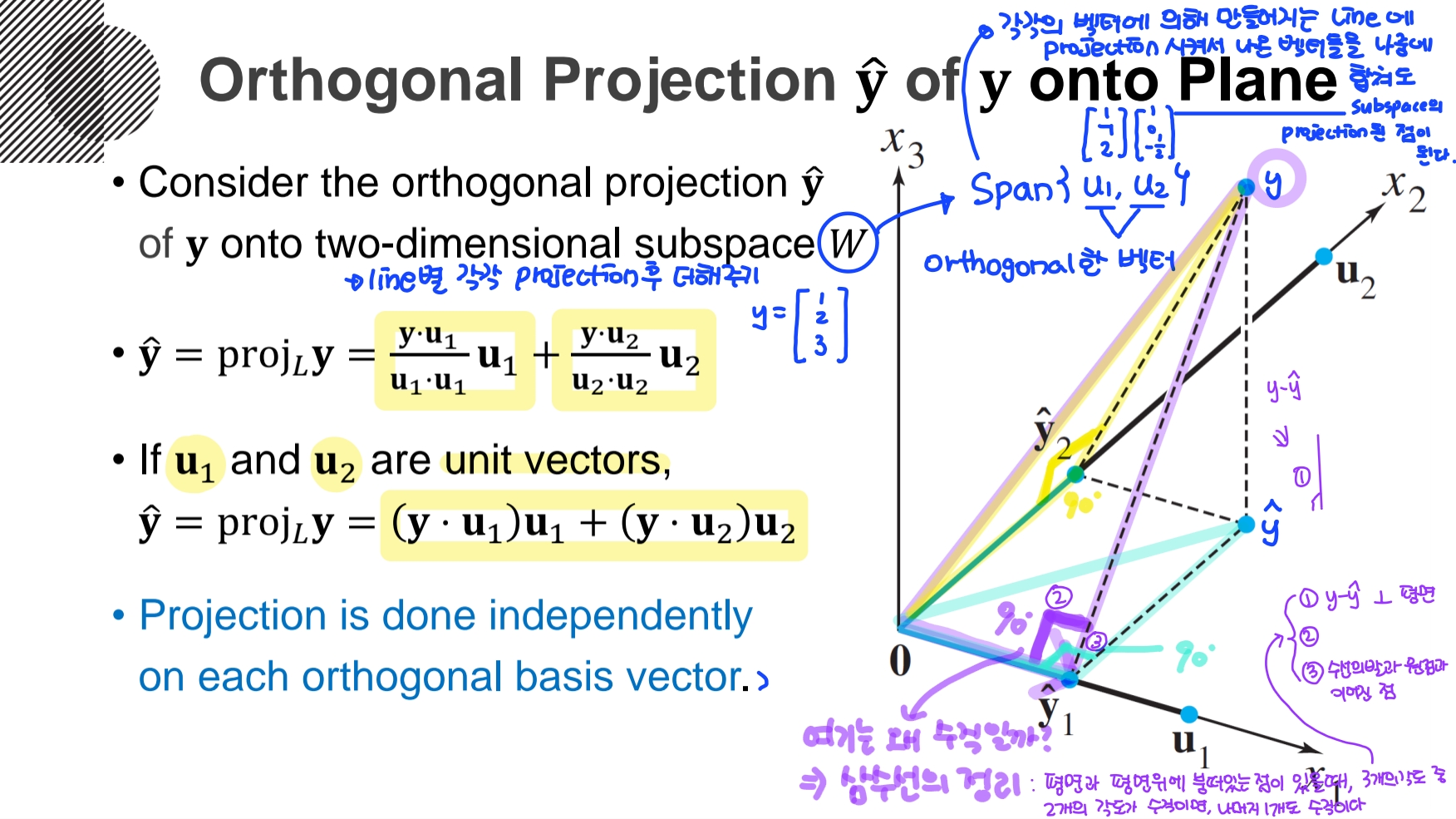
- 2차원 orthogonal set인 subspace W의 Span은 Plane이다. Plane으로의 orthogonal projection은 W의 각각의 벡터에 의해 만들어지는 Line으로의 orthogonal projection을 각각 하고 더해서 구한다.
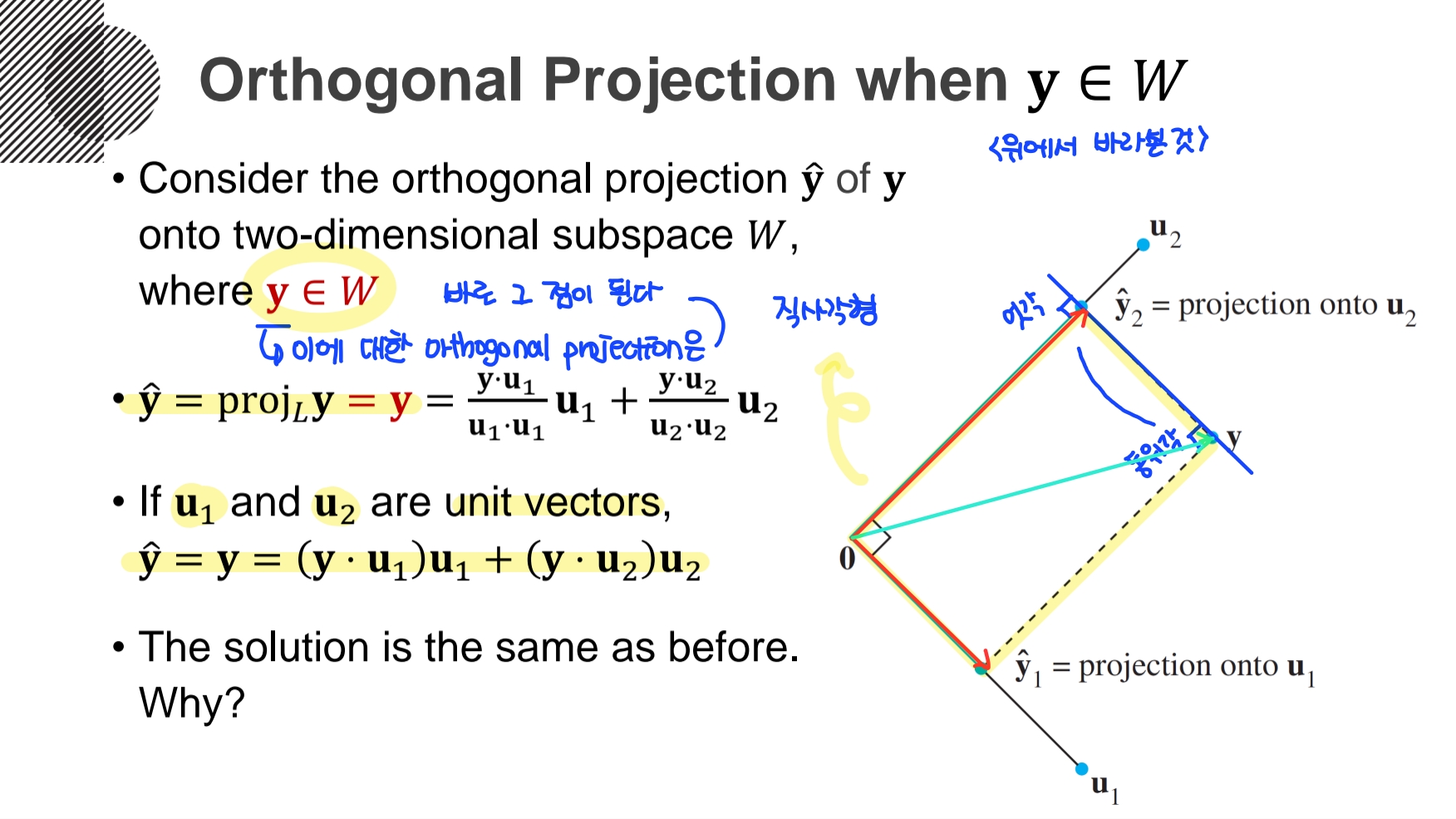
- 2차원 orthogonal set인 subspace W의 Span에 y가 있다면, 이 y에 대한 orthogonal projection은 바로 그 점인 y가 된다. 그리고 y에서 2개의 벡터에 수선의발을 내려 만들어진 평행사변형은 직사각형이 된다.
- Orthogonal Projection Ⅱ
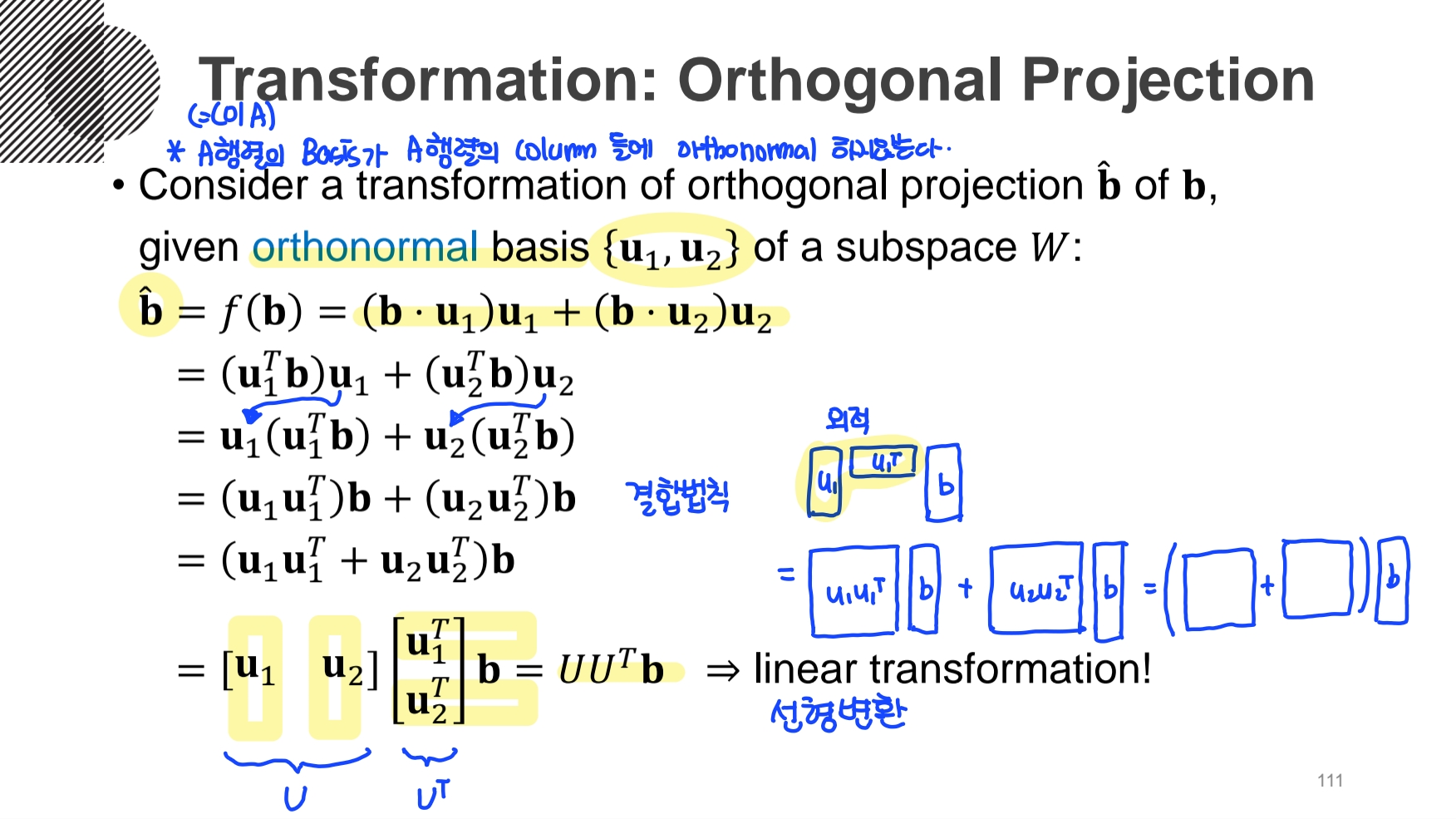
- orthogonal basis를 이용해서 orthogonal projection을 선형변환하여 행렬의 곱으로 유도할 수 있다.
이 과정에서의 마지막에서 아래 이미지의 Sum of outer produncts를 사용하였다.


지난 게시글에 설명한 Normal equation(\(A^TA\hat{x}=A^Tb\))을 이용해서 \(\hat{x}\)를 구했었다. 이를 통해 행렬의 곱으로 유도 가능하다.
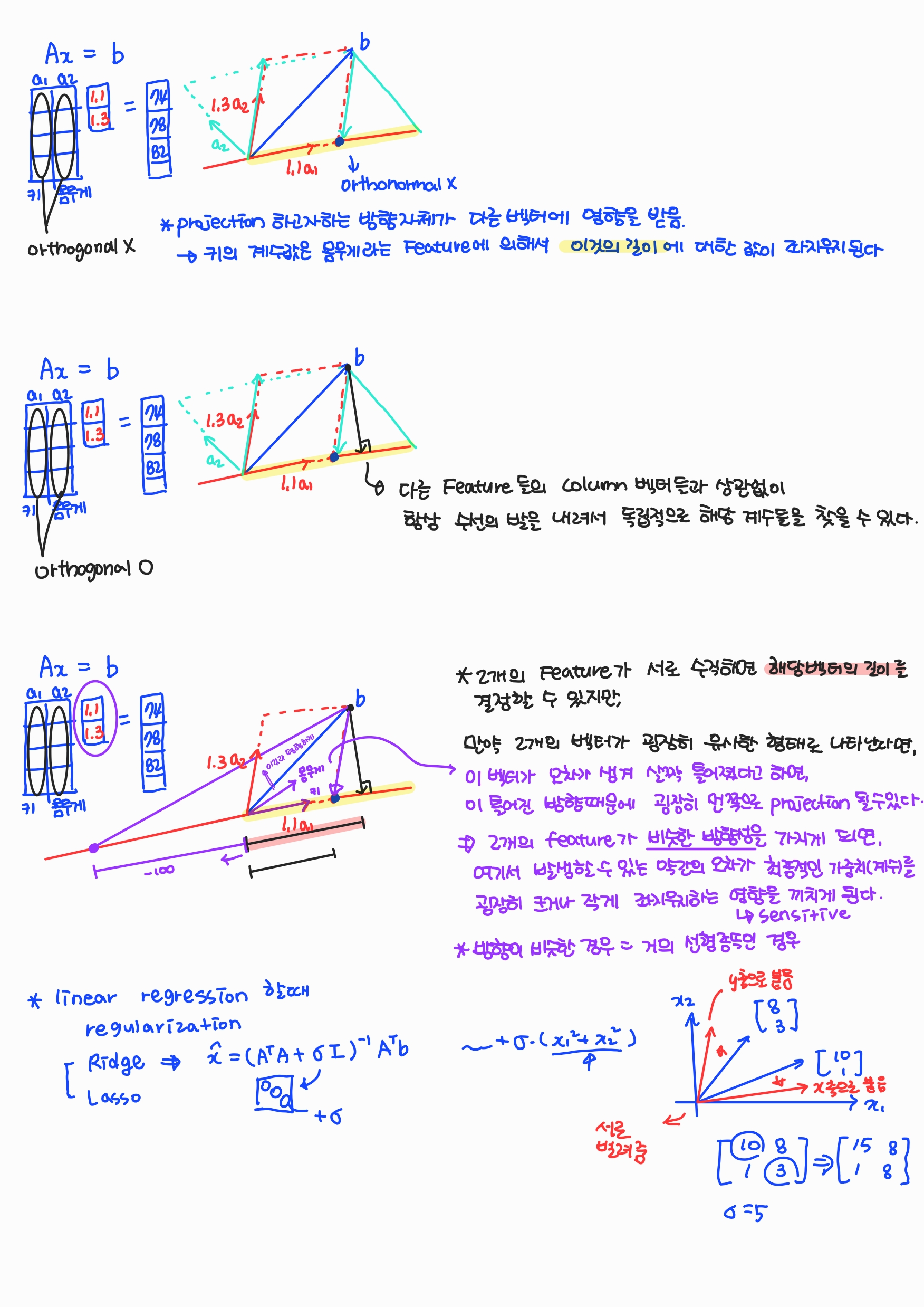
- A 행렬의 벡터들이 서로 orthogonal 하지 않는다면, projection 하고자 하는 방향 자체가 다른 Feature의 벡터에 영향을 받는다.
- A 행렬의 벡터들이 서로 orthogonal 하다면, 다른 Feature 들의 벡터와 상관없이 항상 수선의 발을 내려서 독립적으로 계수를 찾을 수 있다.
- 만약 2개의 Feature의 벡터들이 비슷한 방향성을 가지게 되면(거의 선형종속인 경우), 여기서 발생할 수 있는 약간의 오차가 최종적인 계수를 굉장히 크거나 작게 좌지우지하는 영향을 끼치게 된다. 즉 sensitive 해진다.
이를 해결할 방법으로 Regularization이 있다. 이 방법 중 Ridge(L2 Regularization)은 2개의 Feature간의 correlation을 떨어뜨리기 위해 대각원소에 임의의 σ(감마)값을 한쪽은 x축으로 붙게, 다른 한쪽은 y축으로 붙게끔하여 서로 떨어뜨려준다.
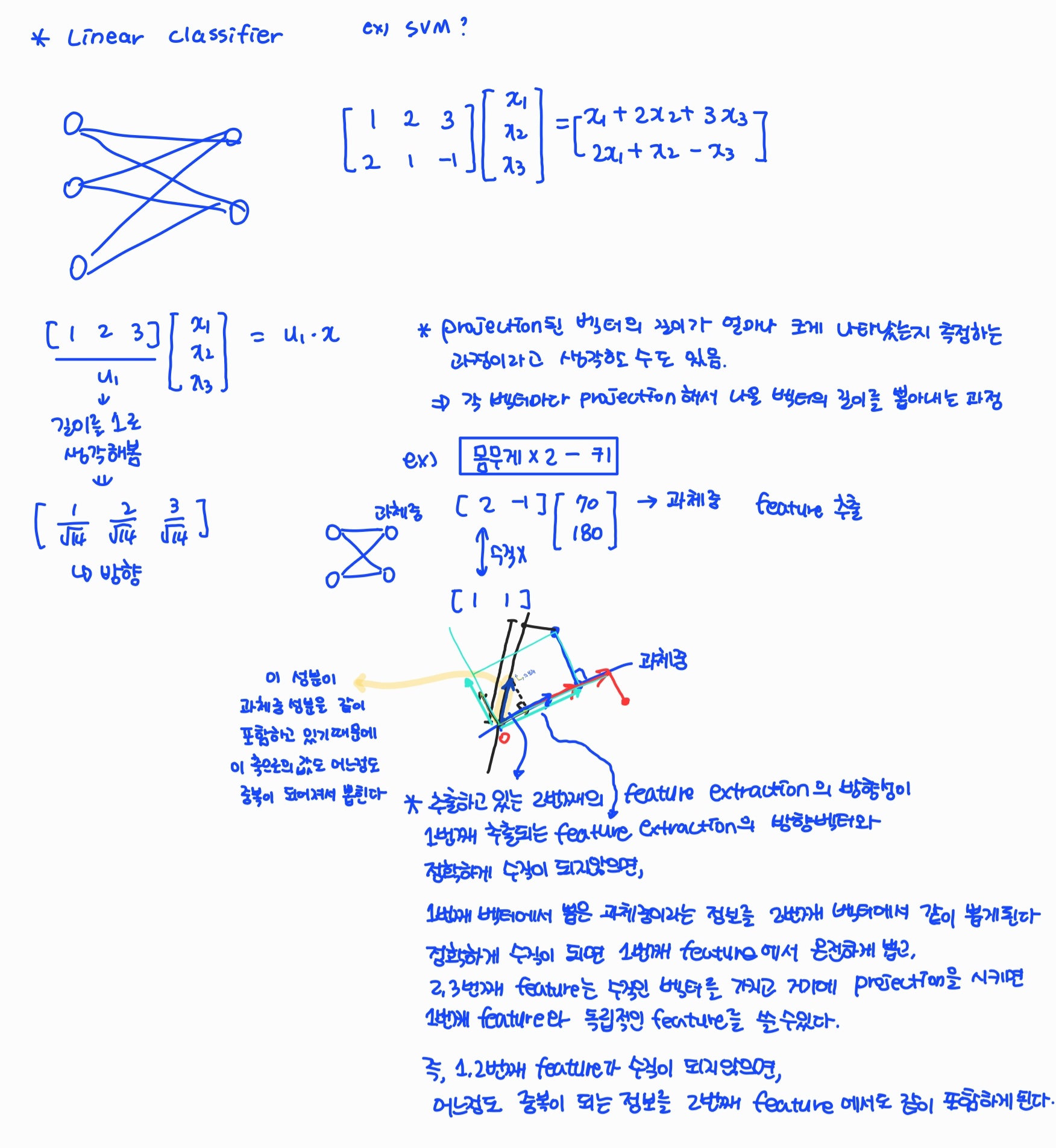
- Linear Classifier
projection된 벡터의 길이가 얼마나 크게 나타났는지 측정하는 과정이라고 생각할 수 있다. 즉, 각 벡터마다 projection해서 나온 벡터의 길이를 뽑아내는 과정이다. 예시로는 SVM이 있다.
'Mathematics | Statistics' 카테고리의 다른 글
| [선형대수학] 인공지능을 위한 선형대수 (8) (0) | 2022.07.21 |
|---|---|
| [선형대수학] 인공지능을 위한 선형대수 (7) (0) | 2022.07.20 |
| [선형대수학] 인공지능을 위한 선형대수 (5) (0) | 2022.07.18 |
| [선형대수학] 인공지능을 위한 선형대수 (4) (0) | 2022.07.17 |
| [선형대수학] 인공지능을 위한 선형대수 (3) (0) | 2022.07.16 |




