[선형대수학] 인공지능을 위한 선형대수 (5)

본 게시물의 내용은 '인공지능을 위한 선형대수(주재걸 교수님)' 강의를 듣고 작성하였다.

해당 글은 아래의 6가지를 다룬다.
1. 내적(Inner Product, Dot Product)
2. 벡터의 길이(Vector Norm)
3. 단위벡터(Unit Vector)
4. 직교벡터(Orthogonal Vectors)
5. Over-Determined System
6. 최소제곱법(Least Squares)
7. 정규방정식(Normal Equation)

 

- Least Squares Problem 소개

- Over-determined Linear Systems

: 방정식의 갯수가 변수의 갯수보다 많을 때(m>n)를 의미한다. 이런 경우 보통 해가 존재하지 않는다.

cf) m=n 일때는 determined, m<n 일때는 Under-determined 라고 한다.

 

- Least Squares의 Motivation

: 해가 없는 경우, 근사적으로라도 solution을 구해보고 싶어서 나오게 됨.

- Inner Product (내적)

: 내적을 행렬의 곱으로 나타내면 $u^{T}v$로 나타낼 수 있다.

- 내적의 성질

  a) 교환법칙O

  b) 분배법칙O

  c) 결합법칙O

  d) 자기 자신(u)과의 내적 결과가 0이라면, u=0 이다. u·u >= 0 이다.

- Vector Norm

: 벡터의 길이를 의미한다. ||v||로 표현한다.

- Vector Norm의 기하학적 의미 : ||cv|| = |c| ||v|| 이다.

- Unit Vector (단위 벡터)

: 벡터의 길이(Norm)가 1인 벡터이다. 벡터의 길이를 1로 바꾸는 과정을 Normalizaing이라고 부른다.

- 벡터간의 거리(Distance)

: dist(u, v) = ||u-v||

- 내적을 이용해 벡터간의 각도를 구하는 방법

: $u·v=||u||||v||cos\theta$ 공식을 통해 각도 θ를 구할 수 있다.

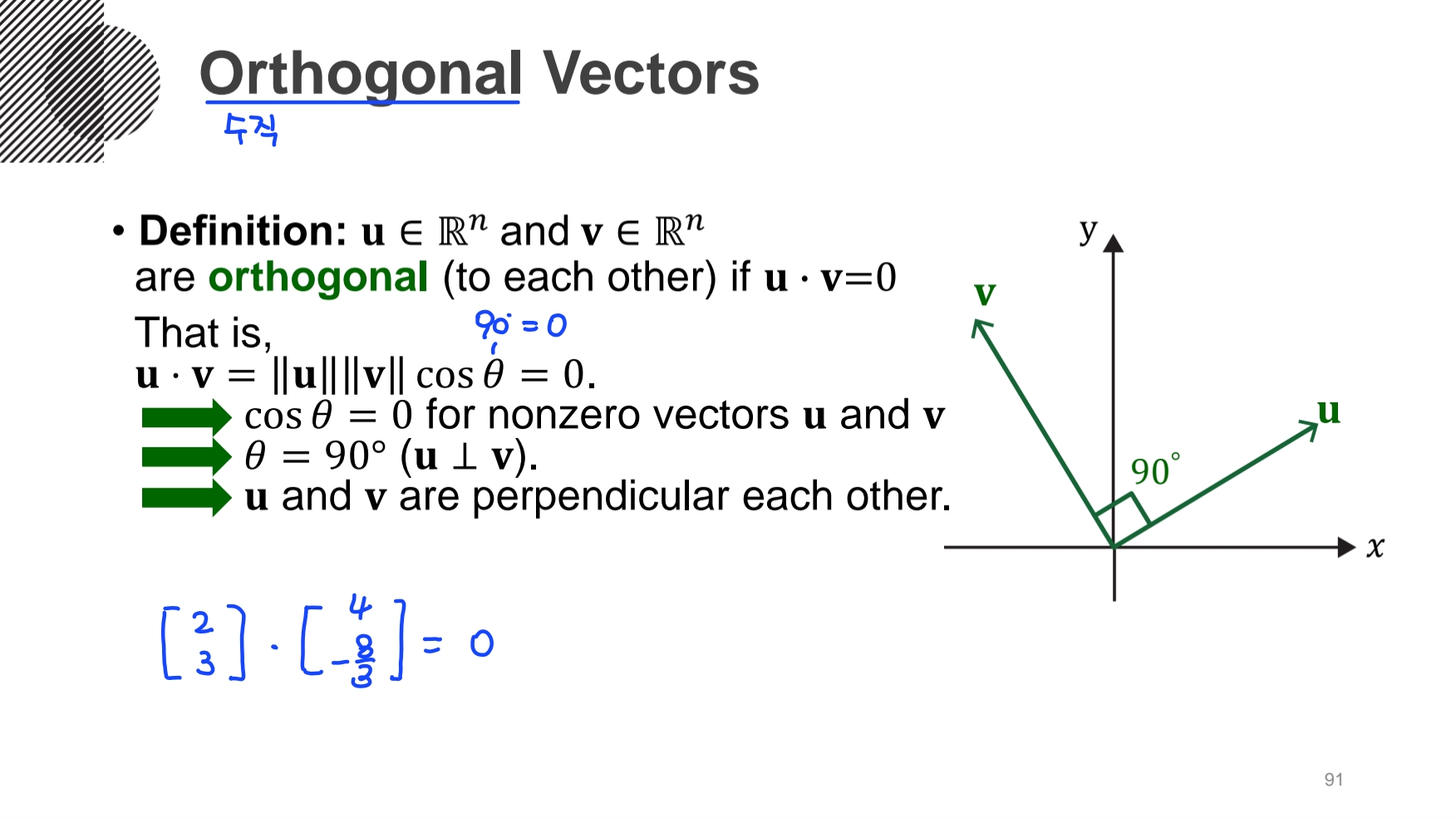
- Orthogonal Vectors (수직 벡터)

: 벡터 u와 v의 내적 결과가 0이라면(u·v = 0), u와 v는 서로 수직 관계이다.

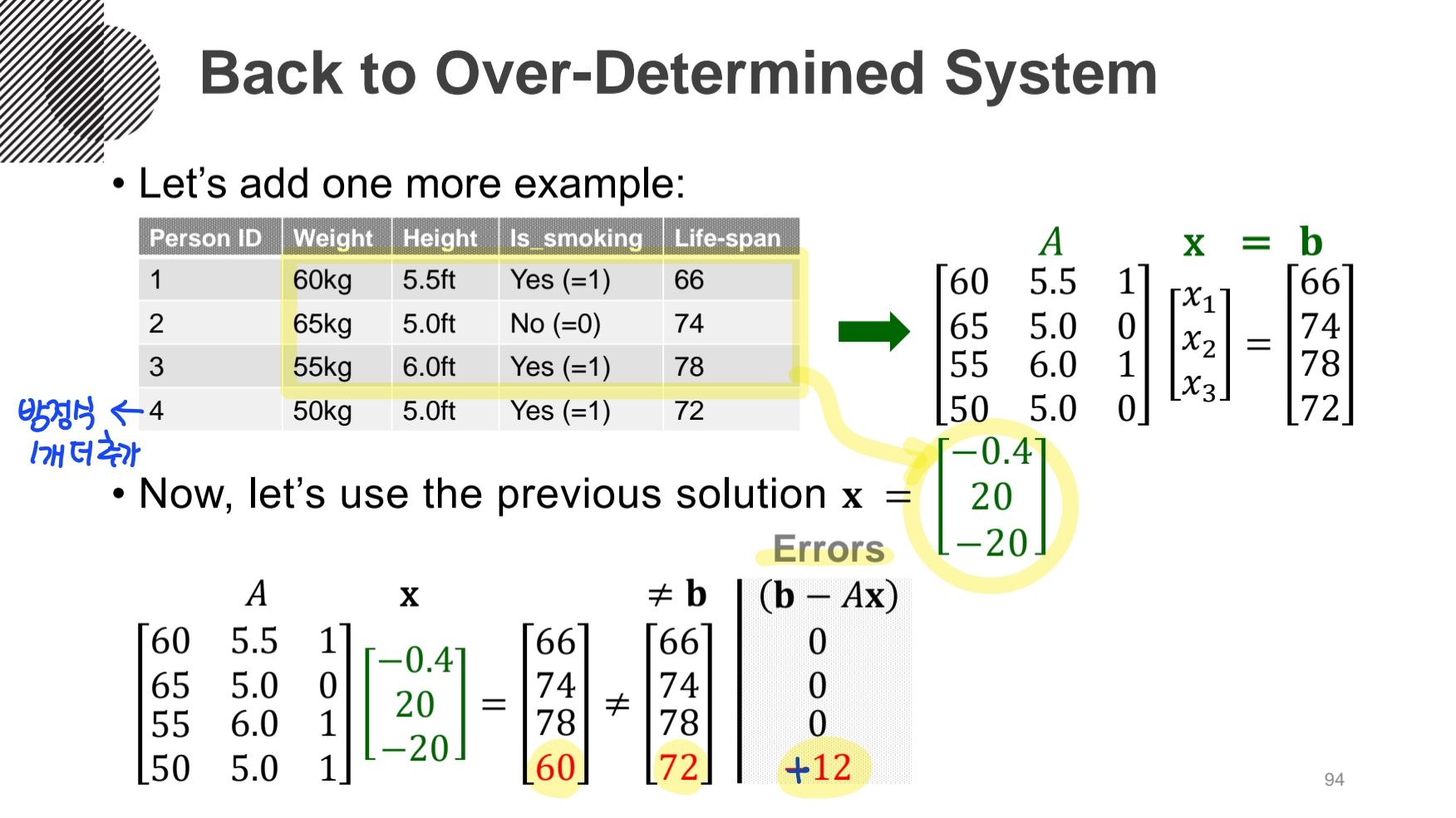
- Least Squares = Sum of squared errors (SSE)

: Errors(b-Ax)의 제곱한 값들의 합에 루트를 씌우는 공식(||b-Ax||)을 통해 Error의 합을 계산한다. 이를 통해 가장 최소값을  더 좋은 solution이라 판단한다. 그래서 Least Squares(최소 제곱)이라 한다. 삭에 완전히 만족하는 해는 못구하더라도, 그 해에 가장 근사하는 해를 구하는 것이다.

- Least Squares Problem : $argmin||b-Ax||$

arg : min||b-Ax||를 만족하는 최적의 값
min||b-Ax|| : 에러를 최소화 하는 값

- Least Squares와 그 기하학적 의미

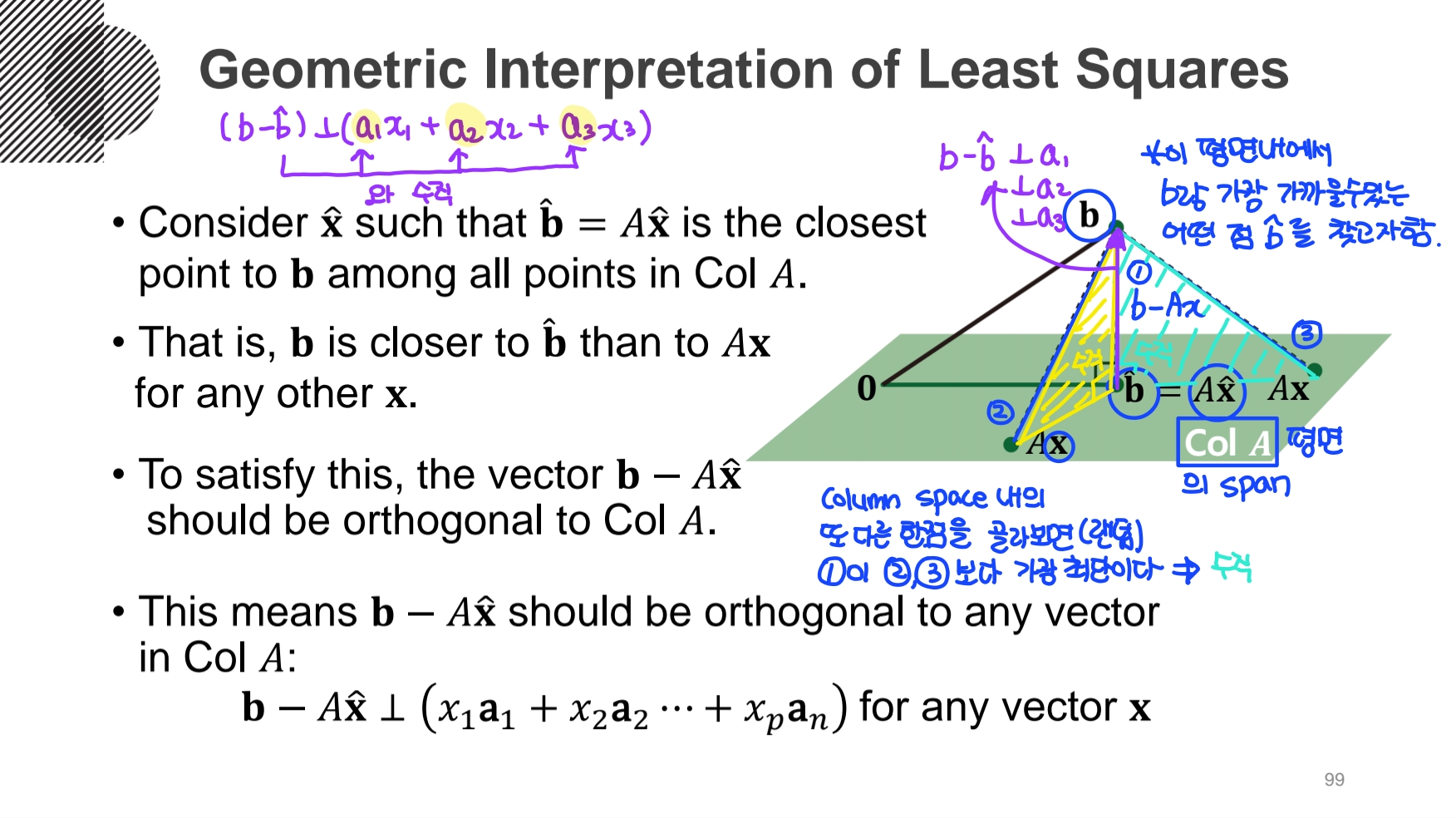
Col A의 Span인 이 평면 내에서 b와 가장 가까울 수 있는 어떤점 $\hat{b}$를 찾고자 한다.

이때 이를 만족하는 평면내의 랜덤한 어떤 x든 Col A 평면과 b-$\hat{b}$은 수직관계이다.

즉, $b-A\hat{x}\perp (x_1{a}_1+x_2{a}_2+...+x_p{a}_n)$

$b-A\hat{x}\perp (x_1{a}_1+x_2{a}_2+...+x_p{a}_n)$ 는 $A^T(b-A\hat{x})=0$ 과 같다.

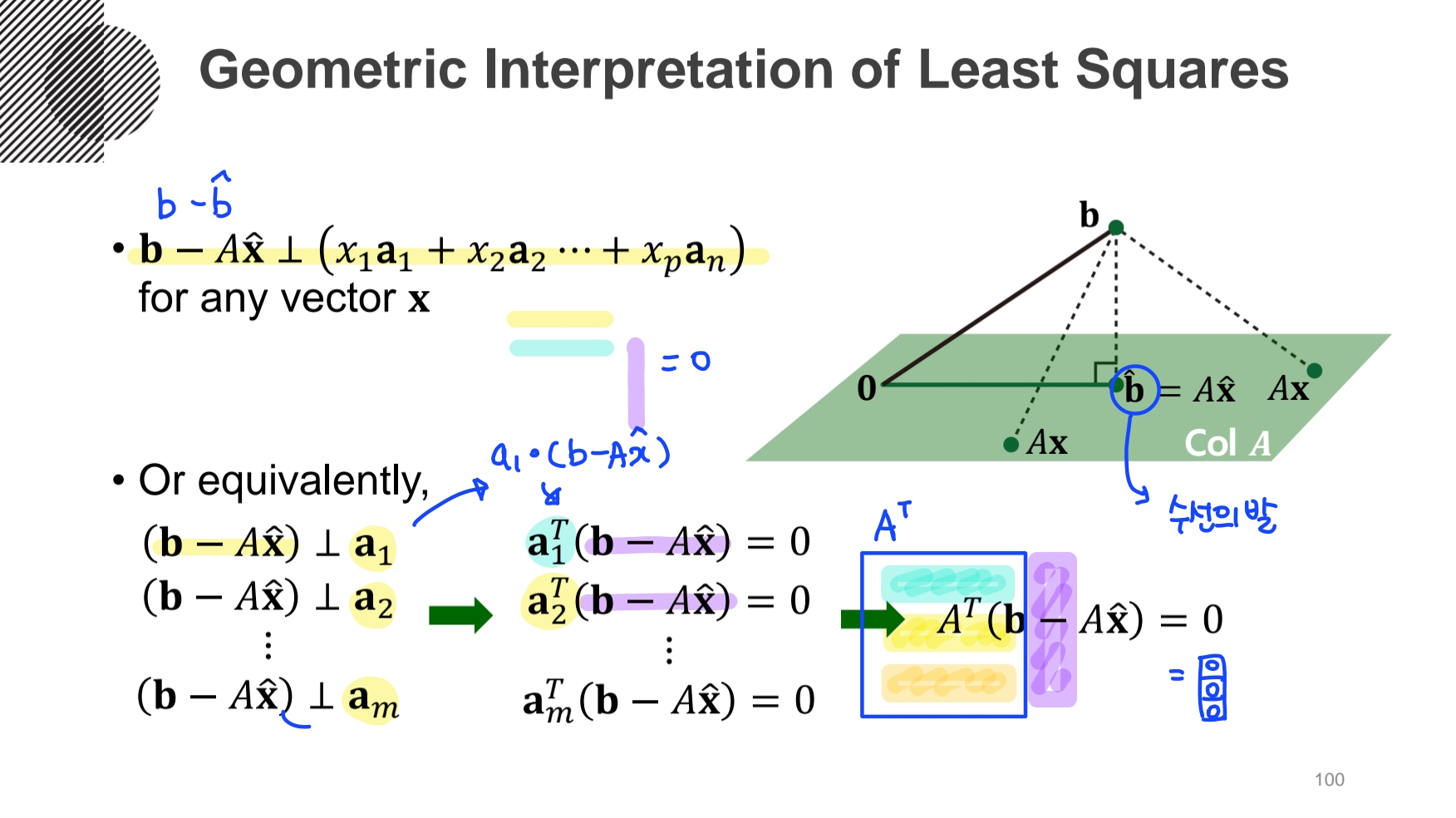
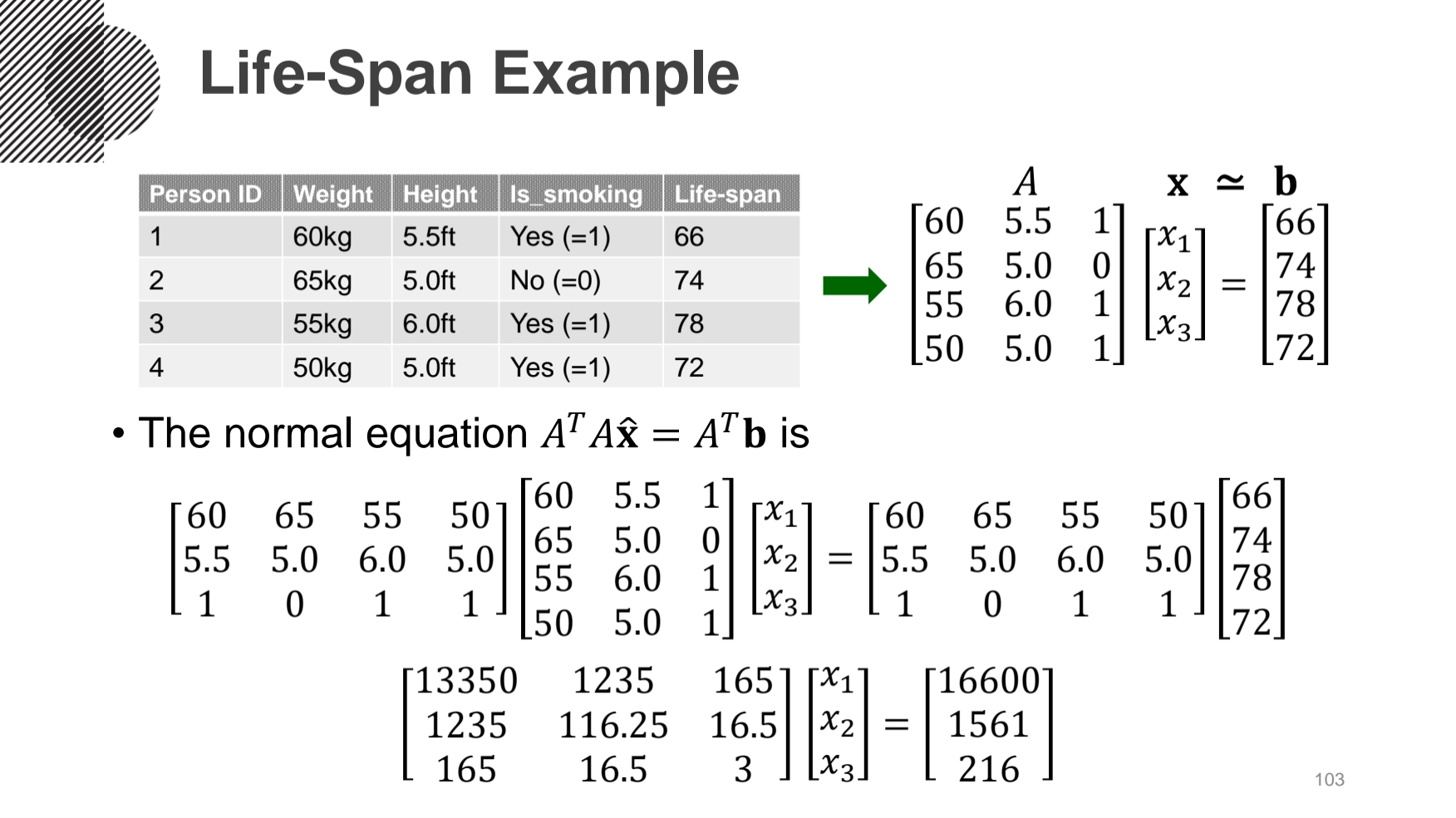
- Normal Equation (정규방정식)

$A^T(b-A\hat{x})=0$ 에서 유도된 식 $A^{T}A\hat{x}=A^{T}b$ 이다. 이를 Normal equation이라 한다.

 

 

 

- 정규방정식

- Normal Equation (정규방정식)을 유도하는 또 다른 방법

$argmin||b-Ax||$에서 $||b-Ax||$가 최소화가 되는 경우에는 $||b-Ax|{|}^2$도 항상 최소가 된다.

그리고 이를 분배법칙으로 결과를 내면 $b^{T}b-x^T{A}^{T}b-b^{T}Ax+x^T{A}^{T}Ax$ 의 식이 완성된다.

$x^T{A}^{T}b,b^{T}Ax,x^T{A}^{T}Ax$의 각각을 x로 미분했을때 결과를 아래에 작성해두었다.

미분결과 $-A^{T}b-A^{T}b+2A^{T}Ax=0$이 나오며 이를 $A^{T}Ax=A^{T}b$로 바꿀 수 있다.

만약 역행렬이 있다면 양변에 $(A^{T}A{)}^{-1}$을 곱해서 x를 구한다.

- 만약 $C=A^{T}A$가 역행렬이 없다면?

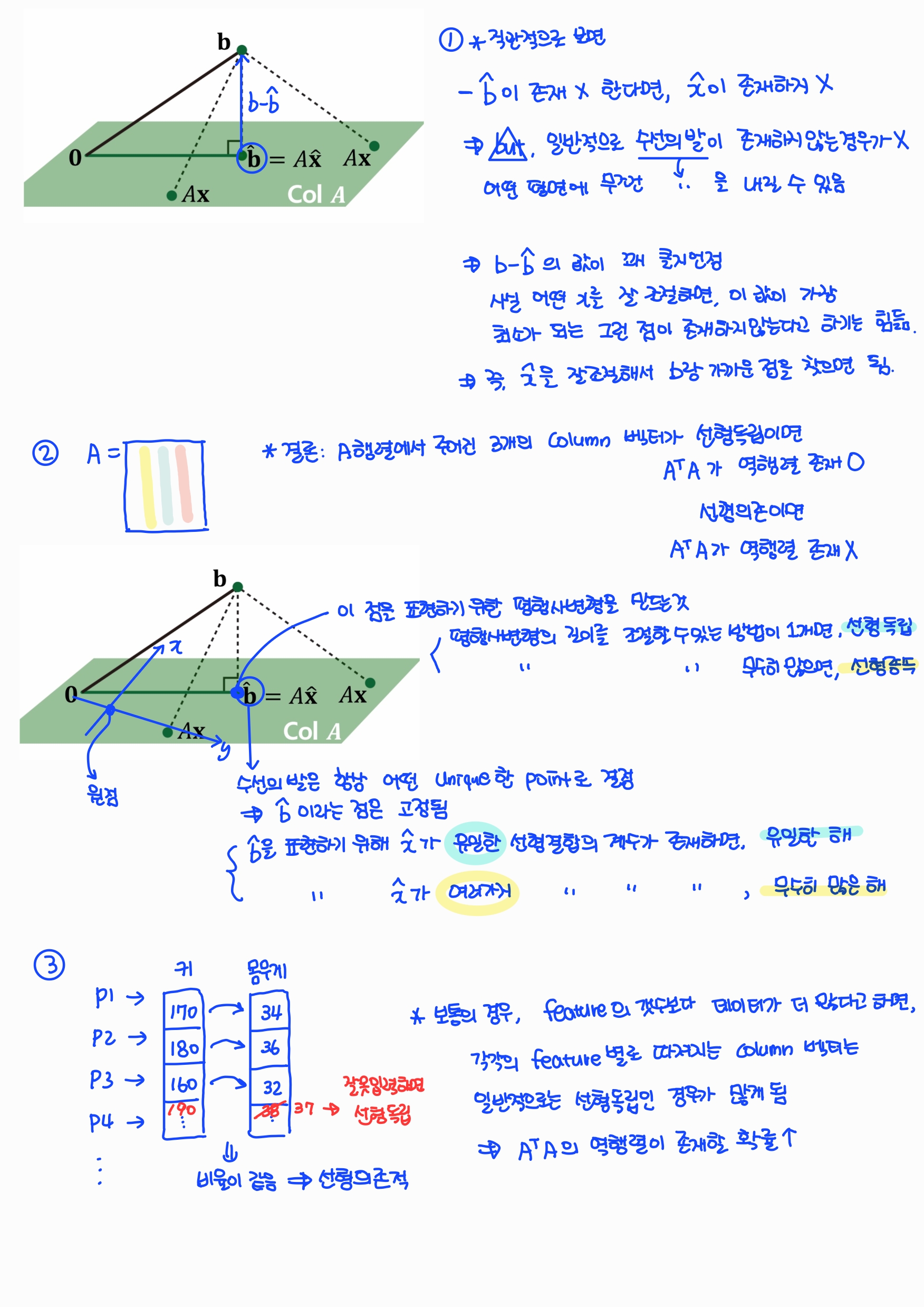
해가 무수히 많다. -> Normal equation에서는 일반적으로 평면에 수직을 내리는 수선의 발이 존재하지 않는 경우는 없다. 즉, 해가 없는 경우는 없다.

 

- 언제 역행렬이 없을까? 

A행렬의 주어진 3개의 Column 벡터가 선형독립이면 역행렬이 존재하고, 선형의존이면 역행렬이 존재하지 않는다.

 

- 그런데, $C=A^{T}A$는 보통 역행렬이 존재하는데 이유는 뭘까?

m>n인 경우, 보통의 경우 각각의 Feature 별로 따져지는 Column 벡터는 선형독립인 경우가 많게 된다.