코딩하는 해맑은 거북이
[선형대수학] 인공지능을 위한 선형대수 (1) 본문
본 게시물의 내용은 '인공지능을 위한 선형대수(주재걸 교수님)' 강의를 듣고 작성하였다.
해당 글은 아래의 5가지를 다룬다.
1. 스칼라(Scalar), 벡터(Vector) 그리고 행렬(Matrix)
2. 열 벡터와 행 벡터(Row Vector, Column Vector)
3. 벡터와 행렬의 연산
4. 선형방정식(Linear Equation)과 선형시스템(Linear System)
5. 항등 행렬(Identity Matrix)과 역행렬(Inverse Matrix)
- 선형대수의 기초

- Vector
: Order가 정해져 있는(크기O, 방향O) 1차원의 숫자 배열로, Row vector와 Column vector 2가지가 있다.

- Column vector
: n개의 행을 가진 n차원 벡터, 보통 default로 Column vector를 사용한다.
- Row vector
: n개의 열을 가진 벡터, Column vector를 정의한 후 transpose한 형태로 정의된다.


- 행렬의 곱셈 2가지
1) 내적 (inner product) : 결과값이 상수
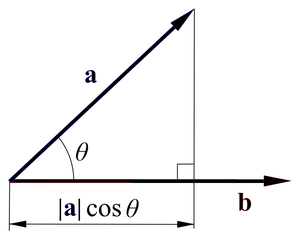
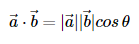
2) 외적 (outer product) : 결과값이 벡터
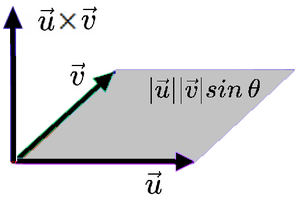
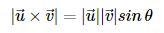

- 행렬의 곱셉에서 교환법칙이 성립되지 않는다.
Q. A와 B가 행렬일 때, AB=BA 인가? (X)

- 행렬의 곱셈에서 분배법칙, 결합법칙이 성립된다.
- 행렬의 곱셈에 전치를 적용할 경우, A와B의 순서가 바뀐다.
(cf. 역행렬의 경우에도 마찬가지)
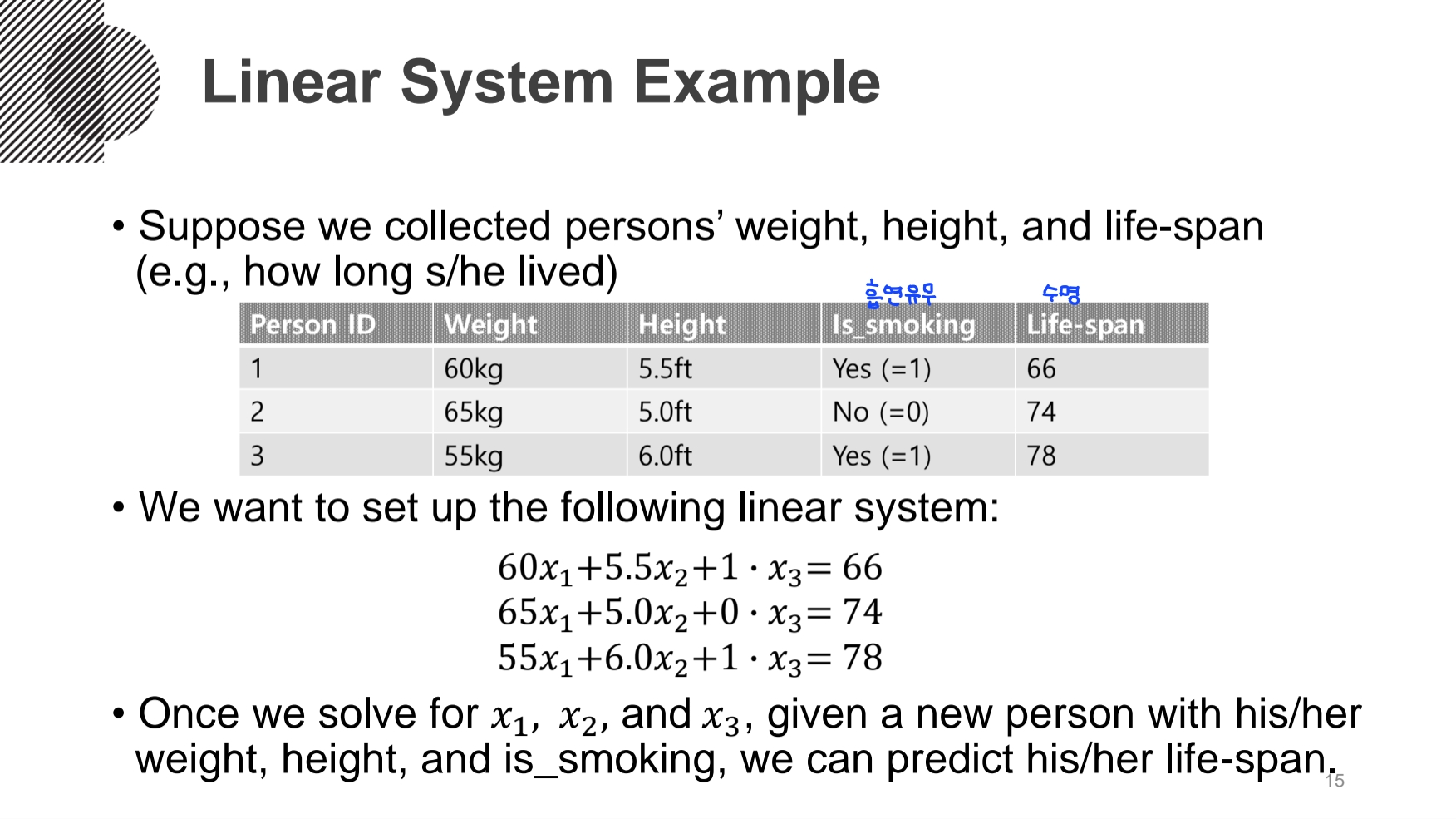
- 선형방정식과 선형시스템

- 선형 방정식(Linear Equation)
: 최고 차수의 항의 차수가 1을 넘지 않는 다항 방정식

- 연립방정식(Linear System == System of Linear equations)
: 방정식의 집합



- 항등 행렬(Identity Matrix) == 단위 행렬(Unit matrix)
: 주대각선의 원소가 모두 1이며 나머지 원소는 모두 0인 정사각행렬이다.
- 항등 행렬이라 불리는 이유
: 어떤 벡터와 곱해도 자기자신을 만들어내기 때문이다.

- 역행렬(Inverse Matrix)
: 어떤 정사각행렬 A와 곱했을 때, 항등행렬이 나오게 하는 행렬을 행렬 A의 역행렬이라 한다.
Q. 역행렬의 정의 조건? 정사각행렬

Q. 역행렬을 이용해서 Ax=b를 푸는 방법은?
: 양쪽에 A의 역행렬을 곱하면, 왼쪽이 항등행렬이므로 x만 남게되어 x=A^-1*b가 나온다.



- 역행렬은 유일한 해를 가진다.
- 2x2 행렬에서 역행렬의 존재 여부는 determinant(det A = ad-bc)로 존재 여부를 확인한다. (det A=0이면 역행렬X)
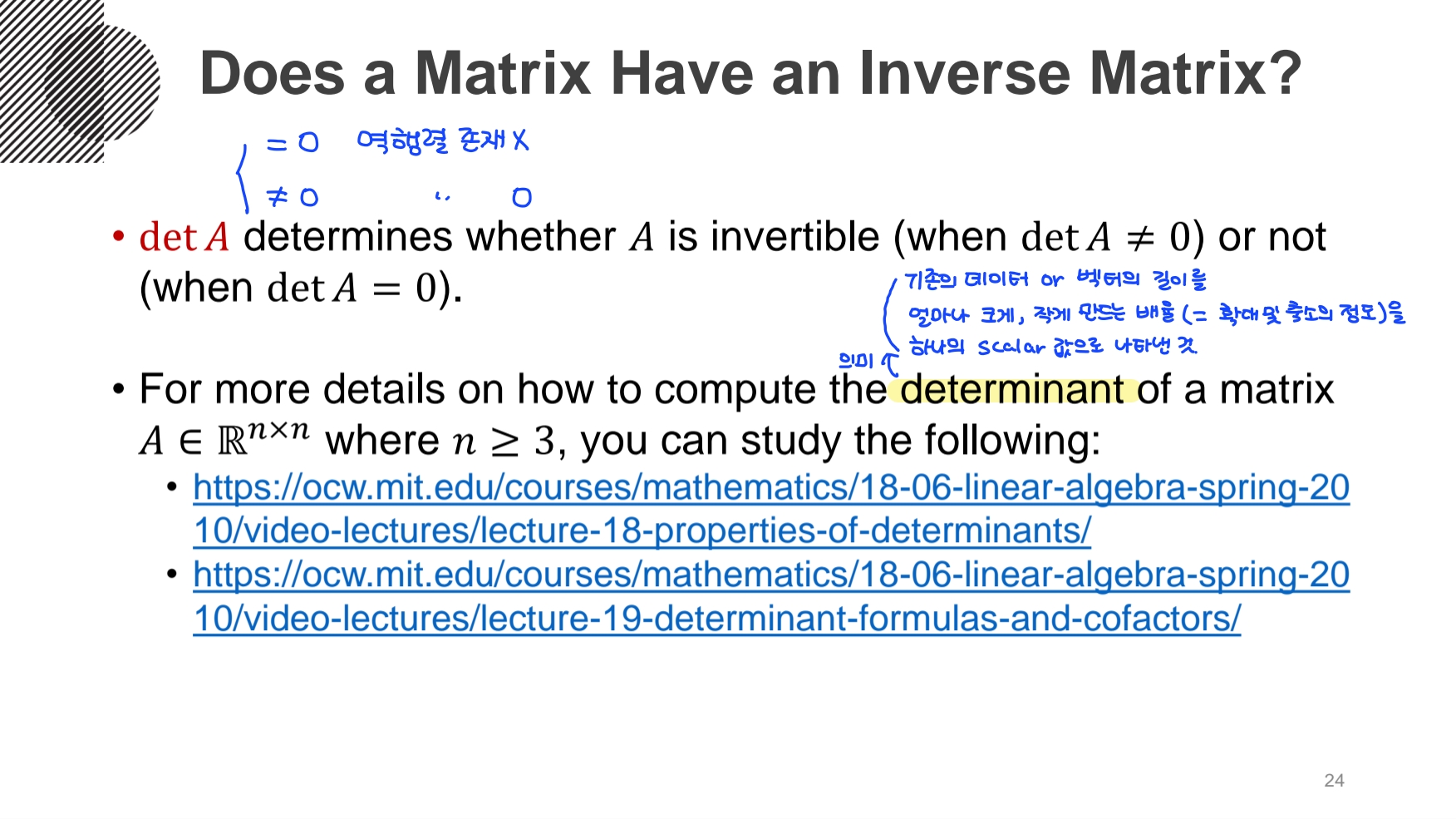
- 역행렬이 존재하지 않는다면, 해가 무수히 많거나 존재하지 않는다.

- 3x3 행렬의 역행렬을 구하는 방법 2가지
https://m.blog.naver.com/jahyone20/220932973637
3x3 역행렬 구하기
역행렬을 구하는 방법에는 크게 2가지가 있다. 1. 가우스 조던 소거법(Gauss-Jordan elimination method)...
blog.naver.com


- 머신러닝에서
1) 해가 무수히 많을 경우, regularization 기술을 사용한다.
2) 해가 없을 경우, least square 방법을 사용한다.
'Mathematics | Statistics' 카테고리의 다른 글
| [선형대수학] 인공지능을 위한 선형대수 (6) (0) | 2022.07.19 |
|---|---|
| [선형대수학] 인공지능을 위한 선형대수 (5) (0) | 2022.07.18 |
| [선형대수학] 인공지능을 위한 선형대수 (4) (0) | 2022.07.17 |
| [선형대수학] 인공지능을 위한 선형대수 (3) (0) | 2022.07.16 |
| [선형대수학] 인공지능을 위한 선형대수 (2) (0) | 2022.07.14 |




