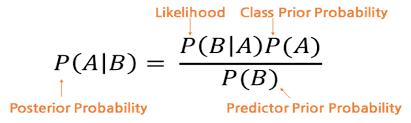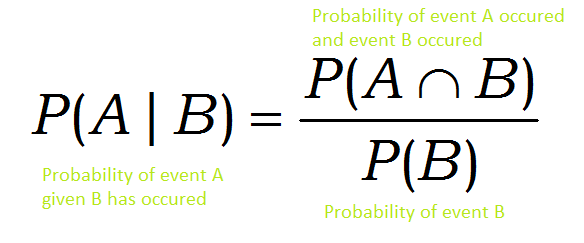코딩하는 해맑은 거북이
[머신러닝] Frequentist(빈도주의) vs Bayesian(베이지안) 본문
해당 글은 Frequentist(빈도주의)와 Bayesian(베이지안)에 대해 다룬다.
Check.
Q. 베이지안과 프리퀀티스트 간의 입장차이를 설명해주실 수 있나요?
베이지안은 사건의 확률을 바라볼 때, 사전 확률을 미리 염두해두고 사건의 발생에 따라 베이즈 정리로 사후 확률을 구해 다시 사전 확률을 업데이트시킨다. 즉, 베이지안은 과거의 사건이 현재 사건에 영향을 끼친다는 입장을 가지고 있다.
반면, 프리퀀티스트는 확률을 무한번 실험한 결과, 객관적으로 발생하는 현상의 빈도수로 바라본다. 즉, 프리퀀티스트는 현재의 객관적인 확률에 의해서만 사건이 발생한다는 입장을 가지고 있다.
Q. “likelihood”와 “probability”의 차이는 무엇일까요?
확률(Probability)은 어떤 시행(trial)에서 특정 결과(sample)가 나올 가능성을 말한다. 즉, 시행 전 모든 경우의 수의 가능성은 정해져 있으며 그 총합은 1(100%)이다.
가능도(Likelihood)은 어떤 시행(trial)을 충분히 수행한 뒤 그 결과(sample)를 토대로 경우의 수의 가능성을 도출하는 것을 말한다. 아무리 충분히 수행해도 어디까지나 추론(inference)이기 때문에 가능성의 합이 1이 되지 않을수도 있다.
PDF(probability density function)에서는 확률변수를 변수로 보기 때문에 총합이 1이지만, likelihood function에서는 분포의 모수를 변수로 보기 때문에 총합이 1이 되지 않을수도 있다.
Frequentist(빈도주의)와 Bayesian(베이지안)은 "확률을 해석하는 관점의 차이"로 나뉜다.
- Frequentist(빈도주의) : 확률을 사건의 빈도로 보는 것.
- Bayesian(베이지안) : 확률을 사건 발생에 대한 믿음(신뢰도) 또는 척도로 보는 것.
Frequentist (빈도주의)
얼만큼 빈번하게 특정한 사건이 반복되어 발생하는가를 관찰하고 가설을 세우고 모델을 만들어서 검증한다.
확률 : 장기적으로 일어나는 사건의 빈도
모수 : 고정된 상수
장점
- 여러번의 실험, 관찰을 통해 알게된 사건의 확률을 검정하므로, 사건이 독립적이고 반복적이며 정규 분포형태일때 사용하는 것이 좋다.
- 대용량 데이터를 처리 할 수 있다면 계산이 비교적 복잡하지 않기 때문에 쉽게 처리가능하다.
단점
- 사전에 관찰지식이 없는 경우 (데이터 부족으로 인한 결과가 적음) 실험 결과의 신뢰가 떨어진다.
- 데이터가 불확실하거나 부족하면 결과가 불확실하다.
예시
1) 동전을 던졌을 때 앞/뒷면이 나오는 사건의 확률
: 동전을 던져 앞면이 나오는 사건의 '확률'은 0.5이다.
2) 검진결과에 의해 암에 걸렸을 확률이 90%이다.
: (의사관점)이러한 검진결과를 가진환자는 정밀검사를 하면 100에 90명은 암에 걸려있다.
3) 화산이 폭발할 확률을 계산 가능한가?
: X, 다양한 요인, 변수들이 많이 때문에 빈도 확률 구하듯이 화산이 폭발할 확률을 구할 수 없다.
4) 각각 나올 수 있는 확률이 동일한 6면 주사위 하나 있을 때, 1의 눈이 나올 확률은?
: 1/6, 6개의 경우들이 확률이 동일하므로(fair), 각각의 경우들을 모두 같은 빈도로 발생한다.
Bayesian (베이지안)
(고정된) 데이터의 관점에서 파라미터에 대한 신념의 변화를 분석한다.
베이지안 방법은 수학적 배경이 까다롭고, 계산량이 많기 때문에 구현의 어려움에 있어서 예전에는 통게학자들로부터 환영받지 못했다. 하지만 컴퓨터의 연산 능력 확장과 다양한 알고리즘 개발로 인해 베이지안 방법도 통계와 머신러닝에서 많이 사용된다.
확률 : 사건 발생에 대한 믿음 또는 척도 (주관적임)
모수 : 확률적으로 변하는 수 (확률변수)
확률적추론 방법
장점
확률 모델이 명확히 설정되어 있다면 조건부로 가설을 검증하기 때문에 가설의 타당성이 높아진다.
단점
사전지식에 대한 모델링이 어렵고 사전지식 모델링에 따른 사후 확률결과가 크게 달라질 수 있다.
예시
1) 동전을 던졌을 때 앞/뒷면이 나오는 사건의 확률
: '앞면이 나왔다'는 주장의 신뢰도가 0.5이다.
2) 검진결과에 의해 암에 걸렸을 확률이 90%이다.
: (환자관점)자신이 암에 걸렸음을 주장하는 의사의 주장이 사실일 가능성(신뢰도)가 90%이다.
3) 화산이 폭발할 확률을 계산 가능한가?
: O, 일어나지 않은 일에 대한 확률의 불확실성의 개념과 사건과 관련있는 여러 확률을 이용해 새롭게 일어날 사건을 추정할 수 있기 때문이다.
4) 각각 나올 수 있는 확률이 동일한 6면 주사위 하나 있을 때, 1의 눈이 나올 확률은?
- 1의 눈이 나올 확률은 0과 1사이의 임의의 값이다. 임의로 1/10이라 간주한다. (사전확률)
- 이 주사위를 실제로 6000번 던졌더니 그 중 992번이 1이 나왔다. (데이터)
- 데이터가 있으므로 새로운 데이터를 이용해서 사전확률을 수정한다. 새로운 확률(사후확률)은 992/6000이다.
* 베이즈 정리(Bayes' theorem) = 베이지안 확률(Bayesian probability)
종속적(의존적) 관계에 놓인 사건들을 기반으로 확률을 구하는 것이고,
조건부 확률로 나타내며, 정보를 업데이트하면서 사후확률을 구하는 것이다.
P(A) : 사전확률(Prior probability), 결과가 나타나기 전에 결정되어 있는 A(원인)의 확률
P(B|A) : 우도확률(Likelihood probability), A(원인)가 발생하였다는 조건하에서 B(결과)가 발생할 확률
P(A|B) : 사후확률(Posterior probability), B(결과)가 발생하였다는 조건하에서 A(원인)가 발생하였을 확률
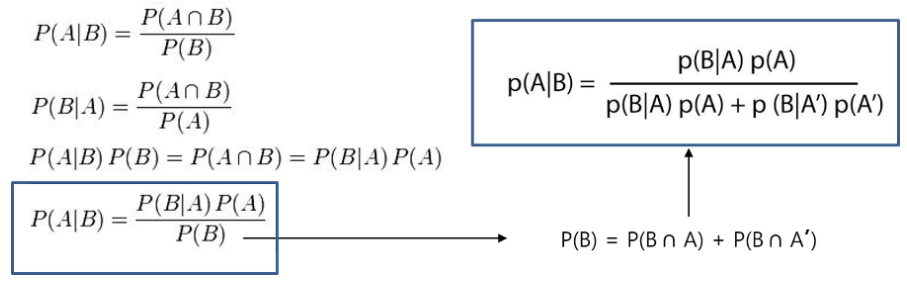
* 조건부확률로부터 베이지안 확률 유도 과정
[참고자료]
https://shawnbaek.tistory.com/14
[Baysian 1] 빈도주의(Frequentist) VS 베이지안(Baysian)
보통 통계학에서 한 사건이 장기적으로 일어날 때 발생하는 빈도를 확률이라고 한다. 확률을 사건의 빈도로 보는 것을 빈도주의(frequentist)라고 하고 확률을 사건 발생에 대한 믿음 또는 척도로
shawnbaek.tistory.com
https://junklee.tistory.com/124
Two kinds of Probabilities. Frequentist vs Bayesian
통계에서 가장 핵심이 되는 키워드인 확률. 이런 확률을 바라보는 관점에는 2가지가 존재한다고 한다. Frequentist 와 Bayesian. 고등수학에서 말하는 수학은 사실 Frequentist에 가깝기 때문에, 두 가지
junklee.tistory.com
https://astralworld58.tistory.com/81
3주차_#2. 베이지안(Bayesian)과 프리퀀티스트(Frequentist) 간의 입장 차이
조건부확률 - B라는 사건이 일어 났을때 A사건이 일어날 확률. 여기서 B라는 사건이 이미 일어난 상황에서 A가 일어 났다는 것은 결국 A와 B가 동시에 일어났다는 것이다. - P(A|B) = P(A∩B)/P(B) (단, P(
astralworld58.tistory.com
https://bioinformaticsandme.tistory.com/47
베이지안 이론 (Bayesian theory)
베이지안 이론 (Bayesian theory) Start. BioinformaticsAndMe 1. 빈도 확률(Frequentist probability) vs 베이지안 확률(Bayesian probability) -빈도 확률(Frequentist probability) > '동전의 앞면' 이 나올..
bioinformaticsandme.tistory.com
'AI' 카테고리의 다른 글
| [머신러닝] 선형회귀(Linear Regression), 로지스틱 회귀(Logistic Regression), 소프트맥스 회귀(Softmax Regression) (0) | 2022.07.27 |
|---|---|
| [머신러닝] 엔트로피(Entropy)와 크로스 엔트로피(Cross-Entropy) (0) | 2022.07.22 |
| [머신러닝] Feature (0) | 2022.07.20 |
| [머신러닝] PCA, SVD, LDA, LSA (0) | 2022.07.18 |
| [머신러닝] Cross Validation (CV, 교차검증) (0) | 2022.07.17 |