코딩하는 해맑은 거북이
[자료구조] 정렬(Sort) 본문
정렬
- 물건을 크기 순으로 나열하는 것 (오름차순 또는 내림차순)
- 정렬은 키(key)가 포함된 레코드들을 순서대로 나열하므로 정렬의 단위는 레코드가 된다.
* 키 : 정렬의 기준 (비교의 대상)
* 레코드 : 하나의 정보단위 (교환의 대상)
ex) 직원정보를 사번으로 정렬 → (키 : 사번, 레코드 : 직원정보 전체)
정렬 알고리즘
- 단순한 코드에 긴 수행시간 : 삽입정렬, 선택정렬, 버블정렬 등
- 복잡한 코드에 짧은 수행시간 : 퀵정렬, 히프정렬, 합병정렬, 기수정렬 등
- 모든 경우에 최적인 정렬 알고리즘은 없다! → 사용되는 환경에 맞추어 선택한다.
- 정렬 알고리즘의 평가로는 (비교횟수, 이동횟수, 안정성)이 있다.
1) 삽입 정렬 (insertion sort)
- 정렬 안 된 부분의 숫자 하나가 정렬된 부분에 삽입됨으로써, 정렬된 부분의 원소 수가 1개 늘어나고, 동시에 정렬이 안 된 부분의 원소 수는 1개 줄어든다.
- 이를 반복하여 수행하면, 마지막엔 정렬이 안 된 부분엔 아무 원소도 남지 않고, 정렬된 부분에 모든 원소가 있게 된다.
- 단, 정렬은 배열의 첫 번째 원소만이 정렬된 부분에 있는 상태에서 정렬을 시작한다.

void insertion_sort(int *list, int n) {
int i, j, next;
for (i = 1; i < n; i++) {
next = list[i];
for (j = i - 1; j >= 0 && next < list[j]; j--) {
list[j + 1] = list[j];
}
list[j + 1] = next;
}
}
2) 선택 정렬 (selection sort)
- 입력 배열 전체에서 최솟값을 ‘선택’하여 배열의 0번 원소와 자리를 바꾸고, 다음엔 0번 원소를 제외한 나머지 원소에서 최솟값을 선택하여, 배열의 1번 원소와 자리를 바꾼다.
- 이러한 방식으로 마지막에 2개의 원소 중 최솟값을 선택하여 자리를 바꿈으로써 오름차순의 정렬을 마친다.

void select_sort(int *list, int n)
{
int i, j, least, temp;
for (i = 0;i < n - 1;i++) {
least = i;
for (j = i + 1;j < n;j++)
if (list[j] < list[least])
least = j;
swap(list[i], list[least]);
}
}
3) 버블 정렬 (bubble sort)
- 이웃하는 숫자를 비교하여 작은 수를 앞쪽으로 이동시키는 과정을 반복하여 정렬하는 알고리즘이다.
- 오름차순으로 정렬한다면, 작은 수는 배열의 앞부분으로 이동하는데, 배열을 좌우가 아니라 상하로 그려보면 정렬하는 과정에서 작은 수가 마치 ‘거품’처럼 위로 올라가는 것을 연상케 한다.

void bubble_sort(int *list, int n)
{
int i, j;
for (i = n - 1; i > 0; i--) {
for (j = 0; j < i; j++) {
if (list[j] > list[j + 1]) {
swap(list[j], list[j + 1]);
}
}
}
}
4) 셸 정렬 (shell sort)
- 버블 정렬이나 삽입 정렬의 오름차순 정렬 수행 과정을 살펴보면, 작은 숫자가 배열의 앞부분으로 매우 느리게 이동하는 것을 알 수 있다.
- 이러한 단점을 보완하기 위해서 삽입 정렬을 이용하여 배열 뒷부분의 작은 숫자를 앞부분으로 ‘빠르게’ 이동시키고, 동시에 앞부분의 큰 숫자는 뒷부분으로 이동시키고, 가장 마지막에는 삽입 정렬(gap=1)을 수행하는 알고리즘이다.
- 간격(gap)이 같은 숫자끼리 그룹을 만들어 각 그룹별로 삽입 정렬하고, gap을 줄여가면서 이 과정을 반복한다. 마지막에는 반드시 간격을 1로 놓고 수행해야한다. 이는 배열 전체를 삽입 정렬하는 것과 같다.

void shell_sort(int *list, int n) {
int cur, k;
for (int h = n / 2; h > 0; h /= 2) {
for (int i = 0; i < h; i++) {
for (int j = h + i; j < n; j += h) {
cur = list[j];
k = j;
while (k > h - 1 && list[k - h] > cur) {
list[k] = list[k - h];
k -= h;
}
list[k] = cur;
}
}
}
}
5) 퀵 정렬 (quick sort)
- 평균적으로 가장 빠른 정렬 방법이다.
cf) 분할정복법 (divide and conquer)
- 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결한다.
- 분리된 문제가 충분히 작지 않으면 재귀호출을 이용하여 다시 분할정복법을 적용한다.
- 퀵 정렬은 전체 리스트를 2개의 부분리스트로 분할하고, 각각의 부분리스트를 다시 퀵 정렬로 정렬한다.
partition() 함수
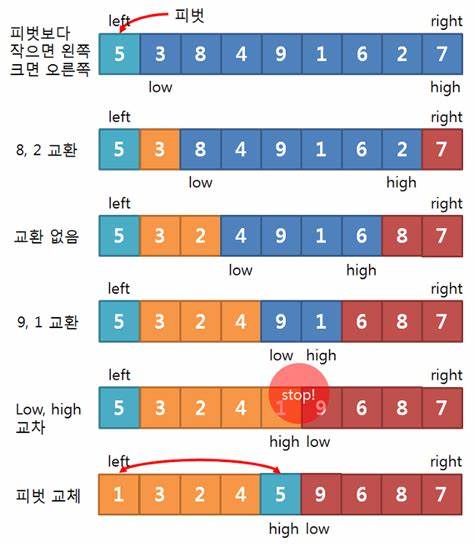
- 피벗 (pivot) : 두 부분의 경계 값 (보통 배열의 가장 왼쪽값으로 선정함)
- 두 개의 인덱스 변수 low와 high를 사용한다.
└ low는 피벗보다 작은 값은 통과, 큰 값을 만나면 정지
└ high는 피벗보다 큰 값은 통과, 작은 값을 만나면 정지
- 정지된 두 인덱스 변수가 가리키는 두 값을 서로 교환하고, low와 high가 교차하면 종료한다.
int partition(int *list, int left, int right) {
int pivot = list[left];
int low = left + 1;
int high = right;
while (low <= high) {
while (pivot >= list[low] && low <= right) {
low++;
}
while (pivot <= list[high] && high >= (left + 1)) {
high--;
}
if (low <= high) {
Swap(list, low, high);
}
}
Swap(list, left, high);
return high;
}
void quick_sort(int list[], int left, int right) {
if (left < right) {
int q = partition(list, left, right);
quick_sort(list, left, q - 1);
quick_sort(list, q + 1, right);
}
}
6) 힙 정렬 (heap sort)
7) 합병 정렬 (merge sort)
8) 기수 정렬 (radix sort)
'Data Structure' 카테고리의 다른 글
| [자료구조] 트리(Tree), 이진트리, 이진트리 순회, 이진탐색트리(BST) (0) | 2023.02.05 |
|---|---|
| [자료구조] 큐(Queue), 원형 큐, 회문 판정 (0) | 2023.02.03 |
| [자료구조] 스택(Stack), 괄호검사, 후위식 계산, 중위식의 후위식 변환 (0) | 2023.02.03 |
| [자료구조] 연결리스트(Linked List) (0) | 2023.02.03 |
| [자료구조] 배열 및 구조체, 다항식 덧셈, 희소행렬 전치 (0) | 2023.02.03 |




