코딩하는 해맑은 거북이
[자료구조] 스택(Stack), 괄호검사, 후위식 계산, 중위식의 후위식 변환 본문
스택 : LIFO (Last-In-First-Out)
기본 연산인 삽입(push)과 삭제(pop)가 한쪽 끝(top)에서만 이뤄지는 순서 리스트
배열 스택 구현
- 스택 구조 정의
#define Max_Stack_Size 10 // 최대 스택크기
typedef int element;
element stack[Max_Stack_Size];
int top = -1;- 공백 상태
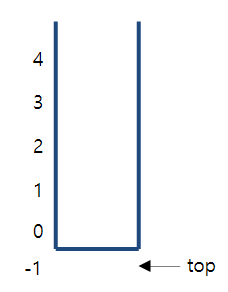
int is_empty()
{
return (top == -1);
}- 포화 상태

int is_full()
{
return (top == (Max_Stack_Size - 1));
}- 삽입

void push(element item)
{
if (is_full()) {
printf("Stack full\n");
exit(1);
}
else stack[++top] = item;
}- 삭제

element pop()
{
if (is_empty()) {
printf("Stack empty\n");
exit(1);
}
else return stack[top--];
}
응용
1. 괄호검사
주어진 입력 문자열에서 왼쪽 괄호와 오른쪽 괄호가 잘 매치되었는지를 검사하는 문제
- 괄호의 종류 : 대괄호 (‘[’, ‘]’), 중괄호 (‘{’, ‘}’), 소괄호 (‘(’, ‘)’)
(ex) ()())( : False
d(ab{cd}) : True
왼쪽 괄호는 push, 오른쪽 괄호는 pop해서 꺼낸 괄호와 종류에 맞게 매치되었는지 검사한다.
그리고 pop할 때 만약 stack이 비어있다면, 이미 매치되지 않은 것이므로 false를 return 한다.
그리고 문자열을 모두 확인하고 난 후에 stack이 비어있다면, 잘 매치된 것이므로 true를 return 한다.
bool paren_matching(char exp[]) { char ch, top_ch; int len = strlen(exp); for (int i = 0; i < len; i++) { ch = exp[i]; switch (ch) { case '(': case '[': case '{': push(ch); break; case ')': case ']': case '}': if (isEmpty()) return false; else { top_ch = pop(); if ((top_ch == '(' && ch != ')') || (top_ch == '{' && ch != '}') || (top_ch == '[' && ch != ']')) return false; } break; } } if (isEmpty()) return true; else return false; }
2. 후위식 계산
후위식이 주어질 경우 스택을 이용해서 계산하는 문제
* 컴퓨터에서 수식의 계산 : 중위식(2+3*4) → 후위식 변환(234*+) → 후위식의 계산(14)
후위식을 차례대로 확인해가며,
피연산자는 push하고, 연산자는 2번을 pop해서 계산한 결과를 다시 push한다.
void Compute_Postfix(char postfix_exp[]) { char ch; int a, b, value; int len = strlen(postfix_exp); for (int i = 0;i < len;i++) { ch = postfix_exp[i]; if (ch != '+' && ch != '-' && ch != '*'&& ch != '/') { value = ch - '0'; push(value); } else { a = pop(); b = pop(); switch (ch) { case '+': push(b + a); break; case '-': push(b - a); break; case '*': push(b * a); break; case '/': push(b / a); break; } } } }
3. 중위식의 후위식 변환
중위식이 주어질 때 스택을 이용하여 후위식으로 변환하는 문제
중위식을 차례대로 확인해가며,
- 연산자 : 해당 연산자를 스택의 연산자와 비교, 우선순위가 높은 연산자 출력, 우선순위가 낮는 연산자는 스택에 저장
- 왼쪽 괄호 : push
- 오른쪽 괄호 : 왼쪽 괄호가 나올 때까지 stack에서 pop하고 출력
- 피연산자 : 해당 피연산자 출력
문자열을 모두 확인하고 난 후에 stack에 남아있는 값들을 차례대로 출력한다.
void Infix_to_Postfix(char infix_exp[], char postfix_exp[]) { char ch, top_op; int temp = 0; int len = strlen(infix_exp); for (int i = 0;i < len;i++) { ch = infix_exp[i]; if (ch == '+' || ch == '-' || ch == '*' || ch == '/') { while (!isEmpty() && (prec(ch) <= prec(peek()))) postfix_exp[temp++] = pop(); push(ch); } else if (ch == '(') push(ch); else if (ch == ')') { top_op = pop(); while (top_op != '(') { postfix_exp[temp++] = top_op; top_op = pop(); } } else postfix_exp[temp++] = ch; } while (!isEmpty()) postfix_exp[temp++] = pop(); postfix_exp[temp] = '\0'; }
'Data Structure' 카테고리의 다른 글
| [자료구조] 트리(Tree), 이진트리, 이진트리 순회, 이진탐색트리(BST) (0) | 2023.02.05 |
|---|---|
| [자료구조] 큐(Queue), 원형 큐, 회문 판정 (0) | 2023.02.03 |
| [자료구조] 연결리스트(Linked List) (0) | 2023.02.03 |
| [자료구조] 배열 및 구조체, 다항식 덧셈, 희소행렬 전치 (0) | 2023.02.03 |
| [자료구조] 자료구조 및 알고리즘 기초 (0) | 2023.02.03 |
Comments




