코딩하는 해맑은 거북이
[머신러닝] Bias-Variance tradeoff, Regularization 본문
해당 글은 아래의 2가지를 다룬다.
1. Bias-Variance tradeoff
2. Regularization
3. Regularization의 종류
Check.
Q. L1, L2 정규화에 대해 설명해주세요.
정규화(일반화)의 목적은 모델이 학습 데이터에 오버피팅되지 않고 처음 보는 테스트 데이터에도 좋은 성능을 내도록 만드는 것이다.
모델의 학습은 loss 함수를 최소화하는 방향으로 진행된다.
이 때, loss 함수에 L1, L2 정규화 항 (norm) 을 더함으로써 모델은 기존의 loss 도 줄이면서 정규화 항 (모델의 피쳐값과 관련) 도 줄이는 방향으로 학습된다.
모델의 피쳐값이 줄어듦에 따라 특정 피쳐가 너무 큰 값을 갖지 않게 되면서 오버피팅을 방지할 수 있게 된다.
L1 정규화 (라쏘 회귀)
L1 정규화는 특정 피쳐의 값이 매우 낮은 경우 (아웃라이어) 0에 수렴되는 특징이 있다. 특정 피쳐가 0이 되어 사라지는 것은 feature selection 과 동일하다고 볼 수 있다.
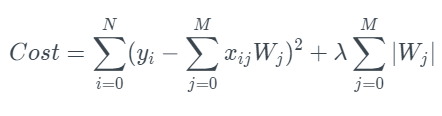
L2 정규화 (릿지 회귀)
L2 정규화는 특정 웨이트의 값이 매우 낮아도 0에 수렴되지는 않고 가까워지는 특징이 있다. 이는 L1 정규화에 비해 강하지 않게 정규화를 실행하여 항상 선형 모델에 일반화 효과를 줄 수 있다.
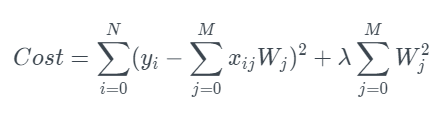
loss 식에 람다 모델의 웨이트에 대한 L1 or L2 norm 을 더해줌으로써 모델의 일반화가 가능해진다.
loss 는 데이터 값과 추정 값의 차이로 모델은 loss 를 최소화하는 방향으로 학습하는데, L1 or L2 정규화를 사용하면 loss 가 웨이트의 크기만큼 커지기 때문에 데이터 값에 예측 값이 fit 해지지 않기 때문이다.
Norm
Norm은 벡터의 크기를 나타내는 것으로 L1 Norm은 벡터의 절댓값 크기를 나타내고, L2 Norm은 직선 거리 (제곱의 루트) 를 나타낸다.
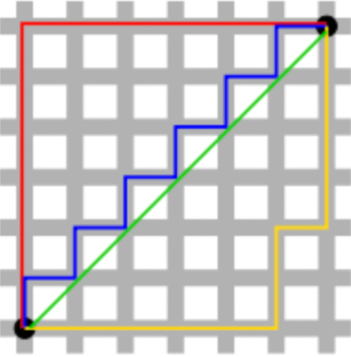
위 그림에서 초록선은 L2 norm 을 의미하고, 나머지 선은 L1 norm 을 의미한다.
L1 loss
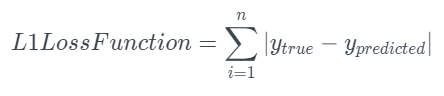
L2 loss
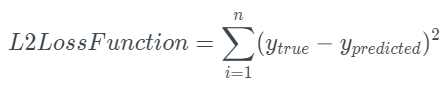
[출처 - AI Tech 면접]
https://boostdevs.gitbook.io/ai-tech-interview/interview/2-machine-learning#21
Q. Bias를 통제하는 방법은 무엇입니까?
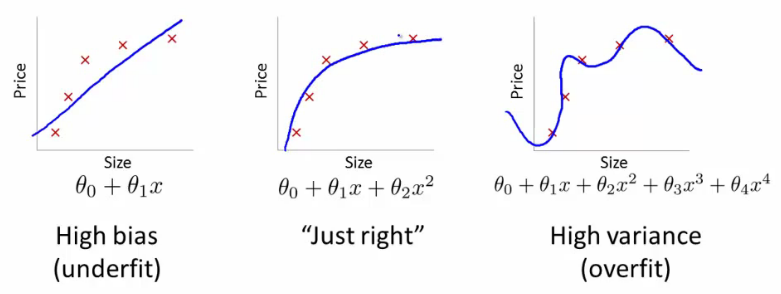
편향(Bias)는 데이터 내에 있는 모든 정보를 고려하지 않음으로 인해, 지속적으로 잘못된 것들을 학습하는 경향을 의미한다. 이는 언더피팅(Underfitting)과 관계되어 있다.
반대로 분산(Variance)는 데이터 내에 있는 에러나 노이즈까지 잘 잡아내는 highly flexible models에 데이터를 피팅시킴으로써, 실제 현상과 관계 없는 랜덤한 것들까지 학습하는 알고리즘의 경향을 의미한다. 이는 오버피팅(Overfitting)과 관계되어 있다.
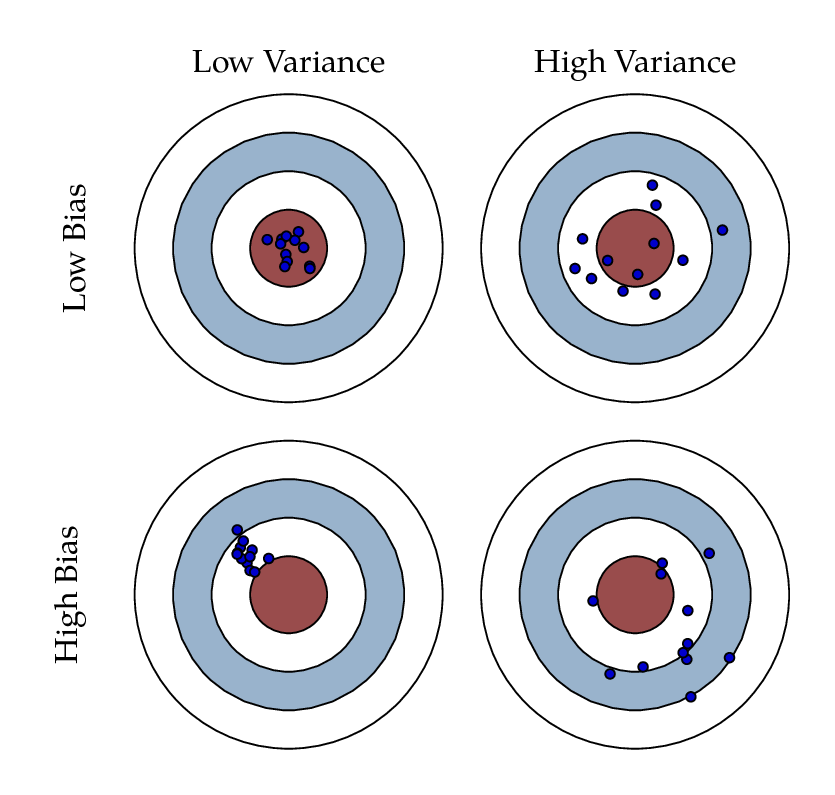
편향(Bias)과 분산(Variance)은 한 쪽이 증가하면 다른 한 쪽이 감소하고, 한쪽이 감소하면 다른 한쪽이 증가하는 tradeoff 관계를 가진다.
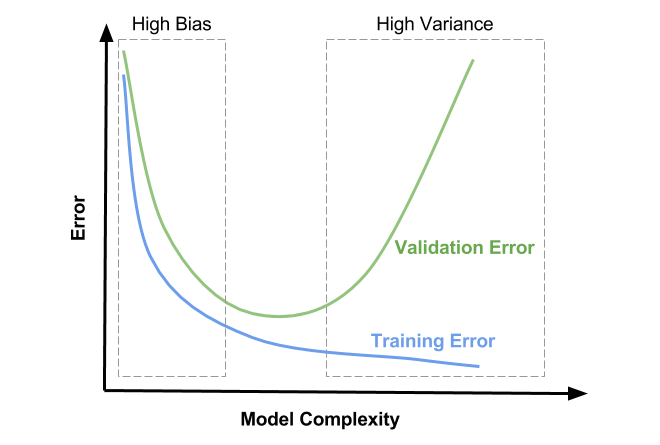
Bias를 통제하기 위한 방법으로는 뉴런이나 계층의 개수가 같은 모델의 크기 증가, 오류평가시 얻은 지식을 기반으로 입력 특성 수정, 정규화, 모델 구조를 수정, 학습 데이터 추가 등의 방법이 있다.
[출처 - AI Tech 면접]
https://boostdevs.gitbook.io/ai-tech-interview/interview/1-statistics-math#22
1. Bias-Variance tradeoff (편향-분산 트레이드오프)
: 새로운 데이터를 모델에 적용했을 때, Bias와 Variance 중 하나가 두드러질 수 밖에 없는 현상을 말한다.
Bias와 Variance를 동시에 최대로 낮출 수 있는 방법은 없다. 내가 얻고자 하는 결과의 특성에 맞추어 Bias와 Variance 정도를 조절하는 것이 최선이다.
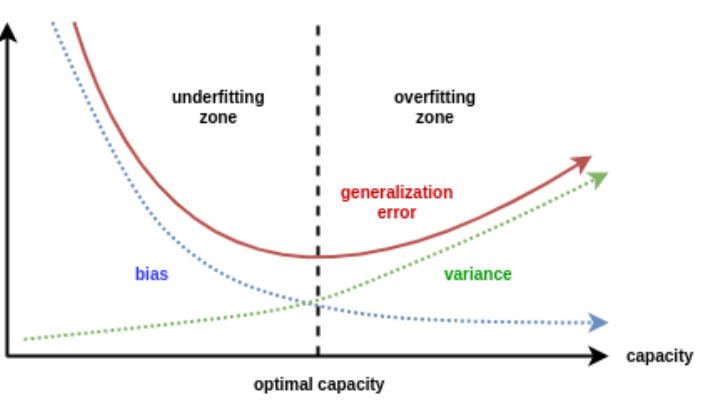
- Bias (편향)
: 한쪽으로 정보가 치우는 것을 의미한다. High Bias와 Low Variance일 경우 모델이 단순하여 underfitting을 초래하고 train, test dataset 모두에서 낮은 정확도를 나타낼 수 있다.
* Bias를 통제하기 위한 방법
- 뉴런이나 계층의 개수가 같은 모델의 크기 증가
- 오류평가시 얻은 지식을 기반으로 입력 특성 수정
- 정규화
- 모델 구조를 수정
- 학습 데이터 추가
- Variance (분산)
: 너무 많은 데이터를 고려해 데이터의 경향성을 제대로 표현하지 못하게 되었을 때를 의미한다. Low bias와 High variance일 경우 모델이 복잡하여 overfitting을 초래하여 train dataset에서는 높은 정확도를 보이지만, 새로운 data에 대해서는 정확도는 현저히 낮다.
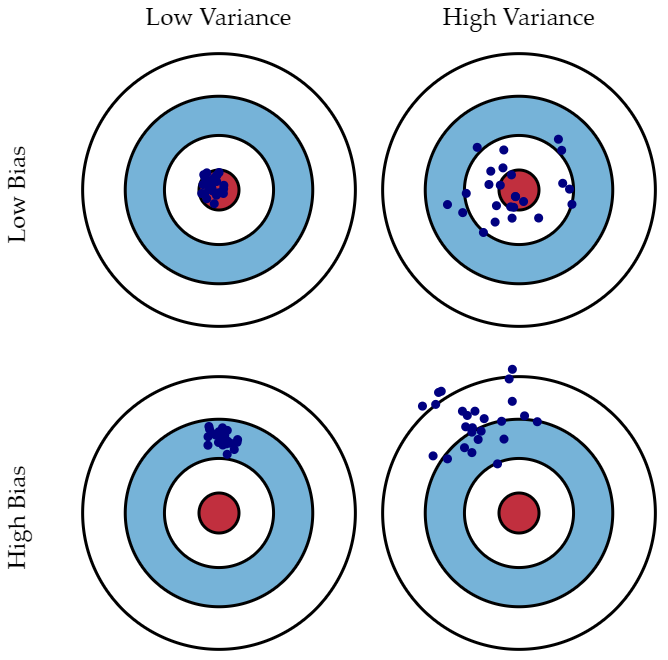
2. Regularization
: overfitting을 방지하기 위해 모델을 제한하는 것을 의미한다. Regularization을 이해하기 위해선 아래의 값들을 먼저 알아야한다.
- Norm
: 벡터의 크기(혹은 길이)를 측정하는 방법(혹은 함수)이다. 두 벡터 사이의 거리를 측정하는 방법이기도 하다.
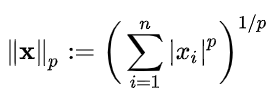
* p는 Norm의 차수를 의미한다. p=1이면 L1 Norm이고, p=2이면 L2 Norm 이다.
* n은 해당 벡터의 원소 수이다.
- L1 Norm
: 벡터 p, q의 각 원소들의 차이의 절댓값의 합이다.
ex) 벡터 p=(3, 1, -3), q=(5, 0, 7) 이라면 p, q의 L1 Norm은 |3-5|+|1-0|+|-3-7|=13
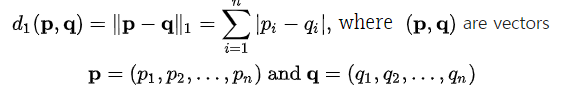
- L2 Norm
: 벡터 p, q의 유클리디안 거리(직선 거리)이다.
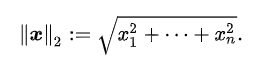
- L1 Loss (= Least Absolute Deviations, LAD)
: 실제값 y_i와 예측값 f(x_i) 사이의 차이값에 절댓값을 취해 그 오차합을 최소화하는 방향으로 loss를 구한다.
이를 Least Absolute Deviations(LAD), Least Absolute Errors(LAE), Least Absolute Value(LAV), Least Absolute Residual(LAR), Sum of Absolute Deviations 라고도 부른다.
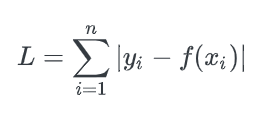
- L2 Loss (= Least Square Error, LSE)
: 실제값 y_i와 예측값 f(x_i) 사이의 오차를 제곱한 값들을 모두 합하여 loss를 구한다.
이를 Least Square Error(LSE) 라고도 부른다.
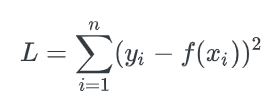
* L1 Loss와 L2 Loss의 차이
L2 Loss는 직관적으로 오차의 제곱을 더하기 때문에 Outlier에 더 큰 영향을 받는다. 즉, L1 Loss가 L2 Loss에 비해 Outlier에 대해서 더 둔감하다라고 표현할 수 있다.
Outlier가 적당히 무시되길 원하면 L1 Loss, Outlier의 등장에 신경써야 하는 경우라면 L2 Loss를 사용하는 것이 좋다.
또한, L1 Loss는 0인 지점에서 미분이 불가능하다는 단점을 가지고 있다.
3. Regularization의 종류
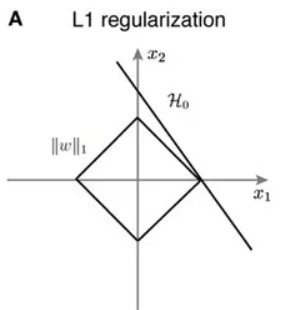
1) Lasso (L1 Regularization)
라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식이다. L2 규제가 회귀 계수 값의 크기를 줄이는 데 반해, L1 규제는 예측 영향력이 적은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것이다. 이러한 특성 때문에 L1 규제는 피처 선택 기능으로도 불린다.
논문에 따라 앞에 분수로 붙는 1/n이나 1/2가 달라지는 경우가 있는데, L1 Regularization의 개념에서 가장 중요한 것은 cost function에 가중치의 절댓값을 더해준다는 것이다.
기존의 cost function에 가중치의 크기가 포함되면서 가중치가 너무 크지 않은 방향으로 학습되도록 한다. 이때 λ는 learning rate(학습률) 같은 상수로 0에 가까울수록 정규화의 효과는 없어진다.
* 특징 : 변수 선택(Feature Selection) 가능, 미분이 불가능하기 때문에 Gradient-base learning에는 주의가 필요하다.
변수 간 상관관계가 높을 때 ridge에 비해 성능이 저하된다.
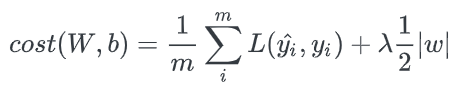
2) Ridge (L2 Regularization)
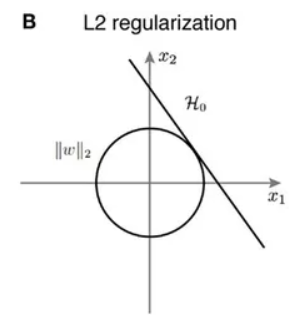
릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델이다. 릿지 회귀는 L2 규제를 적용하는데, L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해서 회귀 계수값을 더 작게 만드는 규제 모델이다.
기존의 cost function에 가중치의 제곱을 포함하여 더함으로써 L1 Regularization과 마찬가지로 가중치가 너무 크지 않은 방향으로 학습하게 된다. 이를 Weight decay 라고도 한다.
* 특징 : 변수 선택(Feature Selection) 불가능, 미분 가능, 변수 간 상관관계가 높은 상황에서 좋은 성능을 보인다.
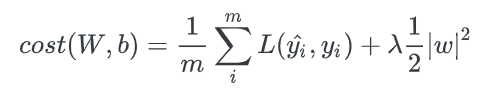
[참고자료]
https://m.blog.naver.com/chocola_meilleure/222217741615
Bias-variance tradeoff(편향-분산 트레이드오프)와 Regularization
☆Bias-variance tradeoff(편향-분산 트레이드오프)란? 학습 알고리즘은 크게 두 종류의 에러를 가집니다....
blog.naver.com
Regularization
Bias-Variance Trade-off 1) 개요 - 아래의 이미지를 통해 bias와 variance의 직관적인 이해를 할 수 있다. 2) Bias (편향) - high bias, low variance일 경우, 모델이 단순하여 underfitting을 초래하고 train,..
sjpyo.tistory.com
https://light-tree.tistory.com/125
딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명
제가 공부하고 정리한 것을 나중에 다시 보기 위해 적는 글입니다. 제가 잘못 설명한 내용이 있다면 알려주시길 부탁드립니다. 사용된 이미지들의 출처는 본문에 링크로 나와 있거나 글의 가장
light-tree.tistory.com
https://seongkyun.github.io/study/2019/04/18/l1_l2/
L1 & L2 loss/regularization · Seongkyun Han's blog
seongkyun.github.io
https://roytravel.tistory.com/57
[머신러닝 이론] 회귀 (Regression)
회귀 소개 회귀는 현대 통계학을 떠받치고 있는 주요 기둥 중 하나이다. 회귀 기반의 분석은 엔지니어링, 의학, 사회과학, 경제학 등의 분야가 발전하는 데 크게 기여해왔다. 회귀 분석은 유전적
roytravel.tistory.com
'AI' 카테고리의 다른 글
| [머신러닝] PCA, SVD, LDA, LSA (0) | 2022.07.18 |
|---|---|
| [머신러닝] Cross Validation (CV, 교차검증) (0) | 2022.07.17 |
| [인공지능기초] Tree Search(Informed Search) (0) | 2022.07.15 |
| [컴퓨터비전] Object Detection, BBOX, Matrix (0) | 2022.07.15 |
| [컴퓨터비전] 컴퓨터비전 문제 영역 (0) | 2022.07.15 |




