코딩하는 해맑은 거북이
인공지능(AI) 기초 다지기 (6) 본문
본 게시물의 내용은 '인공지능(AI) 기초 다지기(부스트코스)' 강의를 듣고 작성하였다.
해당 글은 3-1. Numpy / 벡터 & 행렬 3가지 파트를 다룬다.
1. Numerical Python - Numpy
2. 벡터가 뭐에요?
3. 행렬이 뭐에요?
1. Numerical Python - Numpy
추후 업데이트 예정
2. 벡터가 뭐에요?
- 숫자를 원소로 가지는 리스트(list) 또는 배열(array)
- 공간에서 한 점을 나타낸다.
- 원점으로부터 상대적 위치를 표현한다.
- 벡터에 숫자를 곱해주면(스칼라곱) 길이만 변한다.
- 벡터끼리 같은 모양을 가지면 덧셈, 뺄셈, 성분곱(Hadamard product) 연산을 할 수 있다.

- 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현한다.
- 벡터의 노름(Norm)은 원점으로부터의 거리를 말한다.
L1-노름 : 각 성분의 변화량의 절대값을 모두 더한다.
L2-노름 : 피타고라스 정리를 이용해 유클리드 거리를 계산한다.



- 노름의 종류에 따라 기하학적 성질이 달라진다. 머신러닝에선 각 성질들이 필요할 때가 있으므로 둘다 사용한다.

- L1, L2-노름을 이용해 두 벡터 사이의 거리를 계산할 수 있다. → 벡터의 뺄셈 이용

- 두 벡터 사이의 거리를 이용해서 각도를 계산할 수 있다. 단, L2-노름만 가능하다. → 제2 코사인 법칙 이용


- 내적은 정사영(Orthogonal projection)된 벡터의 길이와 관련 있다.

- 내적은 정사영의 길이를 벡터 y의 길이 ||y|| 만큼 조정한 값이다.

3. 행렬이 뭐에요?
- 행렬(matrix)은 벡터를 원소로 가지는 2차원 배열
- 행렬은 행(row)과 열(column)이라는 인덱스(index)를 가진다.
- 행렬의 특정 행(열)을 고정하면 행(열)벡터라 부른다.
- 전치행렬(transpose matrix)은 행과 열의 인덱스가 바뀐 행렬
- 벡터가 공간에서 한 점을 의미한다면 행렬은 여러 점들을 나타낸다.
- 행렬의 행벡터 \(x_i\)는 i번째 데이터를 의미
- 행렬의 \(x_{ij}\)는 i번째 데이터의 j번째 변수의 값을 말한다.
- 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈, 성분곱(Hadamard product) 연산을 할 수 있다.
- 행렬의 모든 성분에 숫자를 곱해주는 스칼라곱 연산이 가능하다.
- 행렬 곱셈(matrix multiplication)은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.

- 행렬에서 numpy의 np.inner (내적)은 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.
(수학에서 말하는 내적과는 다름)

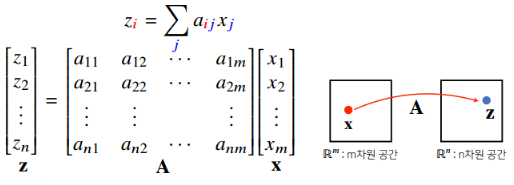
- 행렬은 벡터공간에서 사용되는 연산자(operator)로 이해한다.
- 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
- 행렬곱을 통해 패턴을 추출할 수 있고 데이터를 압축할 수도 있다.
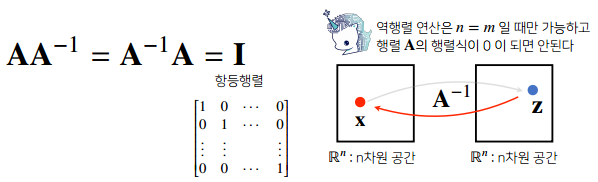
- 역행렬은 어떤 행렬 A의 연산을 거꾸로 되돌린 행렬이다. \(A^{-1}\)라 표기한다.
역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.
cf) numpy.linalg.inv로 구할 수 있음
- 만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 \(A^+\)을 이용한다.
cf) numpy.linalg.pinv로 구할 수 있음

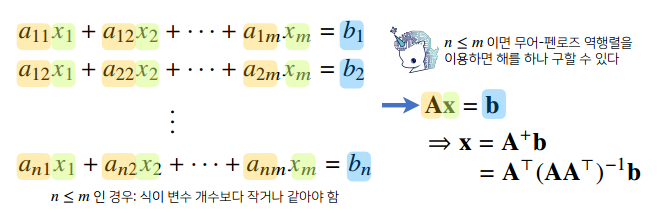
- 응용1 : 연립방정식 풀기
np.linalg.pinv를 이용하면 연립방정식의 해를 구할 수 있다.
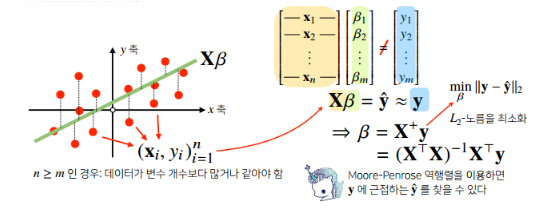
- 응용2 : 선형회귀분석
np.linalg.pinv를 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있다.
cf) sklearn의 LinearRegression과 같은 결과를 가져올 수 있다. 단, y절편(intercept)항을 직접 추가해야 한다.
'AI' 카테고리의 다른 글
| 인공지능(AI) 기초 다지기 (8) (0) | 2022.12.23 |
|---|---|
| 인공지능(AI) 기초 다지기 (7) (0) | 2022.12.19 |
| 인공지능(AI) 기초 다지기 (5) (0) | 2022.12.18 |
| 인공지능(AI) 기초 다지기 (4) (0) | 2022.12.17 |
| 인공지능(AI) 기초 다지기 (3) (0) | 2022.12.13 |




